Esboce o gráfico de
Passo 1
Primeiro, vamos determinar o domínio da função. As restrições são para , pois é quando logaritmo não existe. Então o domínio é
Passo 2
Agora, vamos ver se a função tem alguma paridade, ou seja, se ela é uma função par ou uma função ímpar.
?
Não.
?
Não.
Passo 3
Agora temos que determinar se a função tem assíntotas. Vamos começar pelas verticais. Essas ocorrem perto de pontos de descontinuidade da função. Nesse caso temos o pontos .
Não tem assíntota vertical.
Agora as assíntotas horizontais. Nesse caso, não temos que fazer com pois a função não está definida para .
Também não há assíntota horizontal.
Passo 4
Agora vamos ver crescimento da função. Temos que derivar e ver onde a derivada é positiva e negativa.
Estudando o sinal da derivada temos o seguinte:
para DECRESCENTE
para CRESCENTE
Passo 5
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos.
Como a derivada muda de negativa para positiva em , significa que esse é um mínimo local da função. Podemos descobrir se ele é um mínimo absoluto comparando o valor da função nesse ponto com os valores da função nas fronteiras do domínio. Como
significa que não é mínimo absoluto, visto que a função tende a zero .
Passo 6
Estamos quase terminando. Falta estudar a concavidade da função.
O sinal de se comporta assim:
e
Quando a função tem concavidade para cima
Quando a função tem concavidade para baixo
O ponto é de inflexão.
Passo 7
Compilando todos os dados que descobrimos e o esboço fica assim:
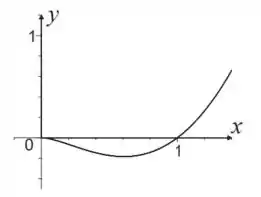
Resposta