Considere a função .
- Determine o domínio de e os pontos de Interseção do gráfico com os eixos coordenados.
- Caso existam, determine as assíntotas horizontais e verticais.
- Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo e os seus valores.
- Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
- Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Passo 1
Vamos letra por letra, porque isso não é bagunça hehe.
- As restrições ao domínio estão localizadas nos pontos de indeterminação ou singularidade. Temos aqui um produto de duas funções sem restrições ao domínio, um polinômio e uma exponencial. Dessa maneira, não haverá restrição ao domínio e:
- Começando pelas assíntotas horizontais, devemos testar a função para e :
- A função cresce quando a derivada é positiva e decresce do contrário. Vamos calcular a derivada então. Pela regra do produto e cadeia:
- A função é côncava para cima quando a segunda derivada é maior que zero e côncava para baixo quando a segunda derivada é menor que zero. Assim, vamos calcular a segunda derivada. Pela regra do produto e cadeia novamente:
- Com os dados obtidos, chegamos ao gráfico:
A interseção com o eixo se dá quando a função vale zero:
Como a exponencial é sempre positiva:
A interseção com o eixo acontece quando , onde, já vimos:
Ou seja, a função passa pela origem.
Passo 2
Já para :
Uma vez que a exponencial vai a zero quando a base tende a menos infinito muito mais rápido que um polinômio vai a menos infinito na mesma condição. Também é possível demonstrar isso usando L’Hôpital.
Dessa maneira, temos uma assíntota horizontal em .
Como a função é sempre continua, não haverá assíntotas verticais.
Passo 3
Que zera em . Testando o sinal à esquerda e a direita desse ponto:
Ou seja, a função é decrescente para:
E crescente para:
Aproveitando os dados que já conseguimos, vimos que a derivada zera em , ou seja, esse é um ponto crítico. Vimos também que a derivada é negativa à esquerda e positiva à direita, assim, pelo teste da primeira derivada esse é um ponto de mínimo. Nesse ponto:
Passo 4
Que zera quando . Testando valores à esquerda e à direta desse ponto:
Portanto, a função é côncava para baixo para:
E côncava para cima para:
No ponto onde a função troca de concavidade, temos um ponto de inflexão:
Passo 5
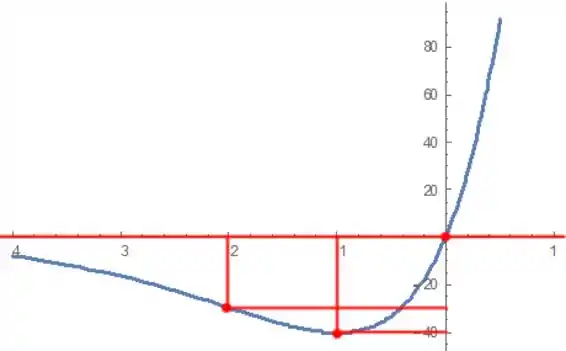
Resposta
Ei, a resposta está no passo a passo :)