Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 691234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a função

f x = x e - x 2 2

  1. Determine as assíntotas horizontais e verticais caso existam.
  2. Determine os intervalos de crescimento e decrescimento, bem como os pontos críticos. Encontre e classifique os extremos relativos de f x .
  3. Determine os intervalos de concavidade voltada para cima e para baixo, indicando os pontos de inflexão.
  4. Esboce o gráfico da função, destacando os elementos encontrados nos itens anteriores.

Passo 1

(a)

Vamos começar pelas assíntotas verticais.

Na expressão da função não tem nenhum termo que possa causar alguma indeterminação (raiz, logaritmo, divisão), então o domínio da f é todo o R → não tem assíntotas verticais. :)

Passo 2

Beleza, agora vamos pras assíntotas horizontais.

Basta calcular os limites no infinito:

lim x → - ∞ ⁡ x e - x 2 2 = - ∞ . 0

Deu indeterminação, então vamos escrever o limite de outra forma:

lim x → - ∞ ⁡ x e - x 2 2 = lim x → - ∞ ⁡ x e x 2 2 = - ∞ ∞

Agora sim, podemos usar l’Hôpital:

lim x → - ∞ ⁡ x e x 2 2 = lim x → - ∞ ⁡ 1 x e x 2 2 = 0

Pro limite em + ∞ , o procedimento vai ser exatamente o mesmo:

lim x → + ∞ ⁡ x e - x 2 2 = lim x → + ∞ ⁡ x e x 2 2 = lim x → + ∞ ⁡ 1 x e x 2 2 = 0

Portanto, y = 0 é assíntota horizontal do gráfico da f .

Passo 3

(b)

Pra estudar o crescimento da função, precisamos da derivada dela. Pela regra do produto:

f ' x = e - x 2 2 + x e - x 2 2 . - x

⇒ f ' x = e - x 2 2 1 - x 2

Passo 4

Vejamos onde essa derivada se anula:

f ' x = e - x 2 2 1 - x 2 = 0

Como a exponencial é sempre positiva, temos

1 - x 2 = 0

x 2 = 1

⇒ x = ± 1

Show, então x = - 1 e x = 1 são os 2 pontos críticos da função.

Passo 5

Agora nos resta classificar esses pontos críticos e assim determinar onde a f está crescendo e onde ela está decrescendo.

Então vamos ver o sinal da derivada!

  • Para x < - 1 :

    • 1 - x 2 < 0

    f ' x = e - x 2 2 1 - x 2 < 0

    → f   é   d e c r e s c e n t e

  • Para - 1 < x < 1 :

    • 1 - x 2 > 0

    f ' x = e - x 2 2 1 - x 2 > 0

    → f   é   c r e s c e n t e

  • Para x > 1 :

    • 1 - x 2 < 0

    f ' x = e - x 2 2 1 - x 2 < 0

    → f   é   d e c r e s c e n t e

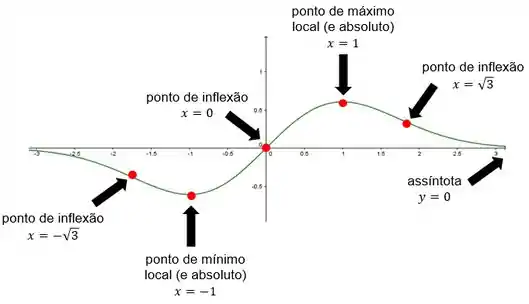
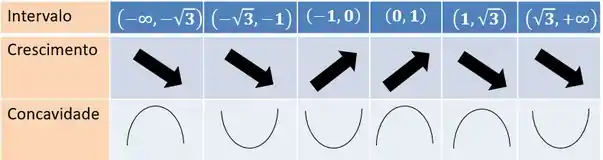
    Resumindo, f é decrescente no intervalo ( - ∞ ,   - 1 ) ∪ 1 ,   + ∞ e crescente no intervalo - 1 ,   1 .

    E pelo teste da primeira derivada, x = - 1 é um ponto de mínimo local e x = 1 um ponto de máximo local.

    Passo 6

    Agora a última etapa: concavidade. Pra ela vamos precisar da segunda derivada, lembrando que:

    f ' x = e - x 2 2 1 - x 2

    Derivando de novo:

    f ' ' x = - x e - x 2 2 1 - x 2 + e - x 2 2 . - 2 x

    f ' ' x = e - x 2 2 - x + x 3 - 2 x e - x 2 2

    ⇒ f ' ' x = e - x 2 2 x 3 - 3 x

    Passo 7

    Vejamos onde a segunda derivada zera:

    f ' ' x = e - x 2 2 x 3 - 3 x = 0

    Como e - x 2 2 > 0 , isso vai dar:

    x 3 - 3 x = 0

    x 3 = 3 x

    x = 0     o u     x 2 = 3 ⇒ x = ± 3

    Então temos 3 candidatos a ponto de inflexão: x = - 3 ,   x = 0 e x = 3 .

    Passo 8

    Então vamos estudar o sinal da segunda derivada nos intervalos - ∞ ,   - 3 , - 3 ,   0 , 0 ,   3 e 3 , + ∞ .

  • Para x ∈ - ∞ ,   - 3 :

    • x 2 > 3

    x 3 < 3 x

    (Tem que trocar o sinal da desigualdade porque x é negativo)

    x 3 - 3 x < 0

    f ' ' x = e - x 2 2 x 3 - 3 x < 0

    → f   t e m   c o n c a v i d a d e   p a r a   b a i x o

  • Para x ∈ - 3 ,   0 :

    • x 2 < 3

    x 3 > 3 x

    x 3 - 3 x > 0

    f ' ' x = e - x 2 2 x 3 - 3 x > 0

    → f   t e m   c o n c a v i d a d e   p a r a   c i m a

  • Para x ∈ 0 ,   3 :

    • x 2 < 3

    x 3 < 3 x

    x 3 - 3 x < 0

    f ' ' x = e - x 2 2 x 3 - 3 x < 0

    → f   t e m   c o n c a v i d a d e   p a r a   b a i x o

  • Para x ∈ 3 , + ∞ :

x 2 > 3

x 3 > 3 x

x 3 - 3 x > 0

f ' ' x = e - x 2 2 x 3 - 3 x > 0

→ f   t e m   c o n c a v i d a d e   p a r a   c i m a

Em cada um dos pontos candidatos a concavidade mudou, então os 3 são pontos de inflexão: x = - 3 ,   x = 0 e x = 3 .

Passo 6

Vamos dar uma resumida no que vimos pra poder partir pro esboço.

A primeira coisa foi a assíntota horizontal y = 0 para x → ± ∞ .

Também estudamos o crescimento e a concavidade da função:

Também ajuda ver que f 0 = 0 , ou seja, o gráfico passa pela origem.

Agora é juntar isso tudo no esboço:

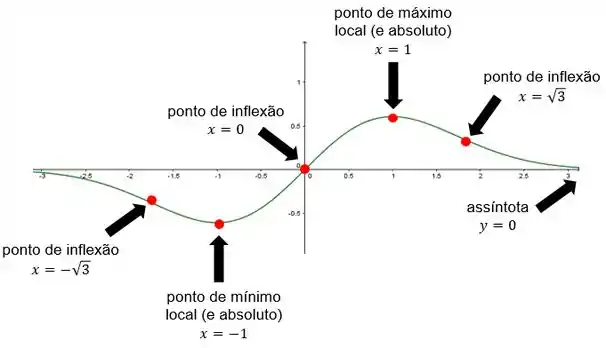
Resposta

(a)

Não tem assíntota vertical. Assíntota horizontal y = 0 .

(b)

Pontos críticos: x = - 1 (mínimo local) e x = 1   (máximo local).

f é decrescente no intervalo ( - ∞ ,   - 1 ) ∪ 1 ,   + ∞ e crescente no intervalo - 1 ,   1 .

(c)

Pontos de inflexão: x = - 3 ,   x = 0 e x = 3 .

f tem concavidade para baixo no intervalo - ∞ , -   3 ∪ 0 ,   3 e concavidade para cima no intervalo - 3 ,   0 ∪ 3 ,   + ∞ .

(d)

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2