Considere a função:
E as suas primeira e segunda derivadas.
a) Ache as assíntotas horizontais e verticais caso existam.
b) Identifique os intervalos onde a função é crescente e onde é decrescente.
c) Encontre os valores máximo e mínimo locais e/ou globais caso existam.
d) Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão.
e) Usando as informações anteriores faça um esboço do gráfico de .
Passo 1
As assíntotas horizontais podem ser encontradas da seguinte forma:
Como ambos limites nos levam a indeterminações do tipo . Por L’Hospital:
Analogamente para o outro limite:
Portanto não existem assíntotas horizontais.
Passo 2
Já para as verticais, podemos observar uma descontinuidade em , logo:
Segue que existe a assíntota vertical:
Passo 3
Os intervalos onde a função é crescente ou decrescente são definidos abaixo:
Portanto, vamos analisar o sinal da derivada:
Como o termo no denominador é um quadrado perfeito, não entra na nossa análise de sinal, por ser sempre positivo. Vamos então analisar o sinal de:
Fatorando:
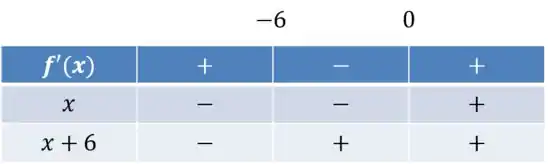 E estudando o sinal pela nossa tabela:
E estudando o sinal pela nossa tabela:
Portanto segue que os respectivos intervalos são:
Passo 4
Em consequência de nossa análise, descobrimos onde a derivada zera, que são os pontos em que e . Portanto são pontos críticos e devemos analisá-los.
Em , temos que a função passa de decrescente para crescente, portanto é um mínimo.
Em , a função passa de crescente para decrescente, portanto se trata de um máximo.
Como a função cresce arbitrariamente para muito grande, e decresce arbitrariamente para muito pequeno, não existe mínimo nem máximo globais.
Portanto é um mínimo local e é um máximo local.
Passo 5
Avaliando o sinal da derivada segunda podemos ver o comportamento da função no que tange à sua concavidade.
Como temos que a nossa derivada segunda é:
Só precisamos analisar o sinal de , que é simples:
Portanto os intervalos são:
Já os pontos de inflexão não existem, pois não conseguimos fazer a derivada segunda zerar:
Passo 6
E o esboço do gráfico é, portanto:
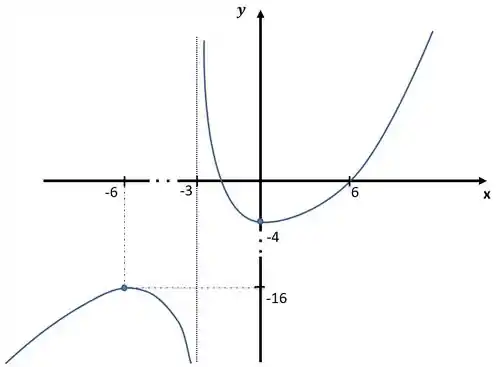
Resposta
Ei, a resposta está no passo a passo :)