Considere a função dada por:
Determine:
Os intervalos onde é crescente, onde é decrescente e os máximos e mínimos locais, caso existam;
Os intervalos onde o gráfico de é côncavo para cima, onde é côncavo para baixo, e as abscissas dos pontos de inflexão, caso existam;
Os extremos absolutos, caso existam.
Passo 1
Cara, quando a gente procura pelo regime de crescimento de determinada função é preciso analisar como se comporta o sinal da derivada dessa mesma função. Onde for positivo cresce, quando negativo, decresce. Dessa forma a gente vê que é necessário derivar . Mas se a gente olhar para a função vai ver que ela é dada por uma soma de uma constante com uma integral! Para derivar integrais assim, como é que fazemos? Chamamos o nosso Teorema Fundamental do Cálculo para ajudar!
Bom, derivado o termo a gente pode observar o seu sinal. Dá para ver que a função tem um denominador que sempre é positivo, já que é composto por uma soma de , que nunca é negativo, com , valor positivo. Dessa maneira, só o numerador influencia no sinal da derivada, de onde a gente tira que para e se . Além disso, a derivada é nula apenas quando , que será uma mínimo local, já que a derivada é negativa antes desse ponto e positiva depois. Não temos pontos de máximo. Conclusão:
Passo 2
Concavidade? Derivada segunda! E partiu usar a Regra do Quociente:
Vamos abrir o polinômio do numerador por Bhaskara:
O sinal só depende do numerador, já que o denominador está elevado a um expoente par. Vamos fazer o quadro de sinais então para a derivada segunda, de onde tiraremos a concavidade do gráfico:
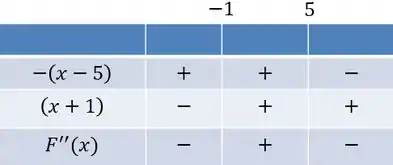
Dá para concluir que a concavidade é para baixo quando e para cima no intervalo . Temos pontos de inflexão em e .
Passo 3
Para saber se , ponto de mínimo local que achamos na letra é mínimo global (absoluto) basta pensar que se a derivada antes desse ponto é sempre negativa e depois é sempre positiva, como calculamos, não havendo descontinuidades no domínio, teremos que antes e depois desse valor só teremos valores acima de . A conclusão é que, pelas circunstâncias, será sim um ponto de mínimo absoluto!
Não haverão pontos de máximo (local ou absoluto).