Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa função aqui
E pediu para determinarmos várias coisas! Aqui vou fazer um resumo de cada uma dessas coisas e como encontramos cada uma delas:
- Pontos críticos: pontos onde a derivada é nula
- Máximos e mínimos locais: pontos onde a derivada apresenta troca de comportamento (de positivo/negativo para negativo/positivo)
- Intervalos de crescimentos e decrescimento: crescimento – intervalo onde a derivada é positiva, decrescimento – intervalo onde a derivada é negativa
- Pontos de inflexão: onde a segunda derivada é zero
- Concavidade da função: côncava para cima – derivada segunda positiva; côncava para baixo – derivada segunda negativa;
- Assíntotas verticais: pontos em que o denominador da função é zero; Assíntotas horizontais: comportamento da função quando
Anota aí!

E é tudo isso que vamos fazer! Vamos começar analisando as assíntotas, depois analisando a derivada primeira, a derivada segunda e por fim construir esse gráfico bem bonitão!
Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Nossa função é
Existir assíntota vertical depende de termos uma descontinuidade da função. Mas nesse caso sabemos que a função arco cosseno é bem-comportada! Sendo assim não temos assíntotas verticais

Para verificar assíntotas horizontais precisamos calcular o limite da função quando , beleza? Mas nossa função é definida apenas entre então aqui também não temos assíntotas horizontais

bora analisar a derivada primeira?
Passo 3
Agora vamos analisar a derivada :
Os pontos críticos são onde a derivada é zero:
Aqui não temos nenhum valor que possa ser substituído em ali na derivada que possa anular essa expressão! Sendo assim, não temos pontos críticos!
Tudo bem até aqui?

Agora vamos ver o último quesito que envolve a derivada: intervalo de crescimento e decrescimento!
Temos que a função é decrescente quando a derivada é negativa, então nesse caso
Notem que a derivada sempre assume valores negativos, então a função é sempre decrescente!
 Tudo bem até aqui?
Tudo bem até aqui?
Bora para a análise da derivada segunda!
Passo 4
Agora vamos analisar os aspectos que envolvem a derivada segunda! Com a derivada segunda podemos encontrar os pontos de inflexão, ou seja, os pontos onde a concavidade da função muda!
A ideia é análoga ao da derivada primeira: pegar a derivada segunda, igualar a zero e encontrar os pontos que satisfazem isso. Por fim, analisar o sinal da em torno desses pontos e encontrar a concavidade da função
- Derivada segunda positiva: função côncava para cima
- Derivada segunda negativa: função côncava para baixo
Beleza?

Vamos resgatar a derivada primeira do passo anterior:
E derivar novamente
Igualando a zero temos:
E assim temos apenas uma solução:

Esse é nosso único ponto de inflexão!
Agora vamos analisar o sinal da derivada segunda em torno desse ponto.
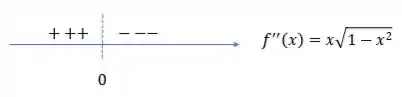
Em resumo temos
Beleza? Estamos quase lá!

Passo 5
Nosso passo final é reunir todas as informações e esboçar o gráfico da função!
E nosso gráfico ficou assim:
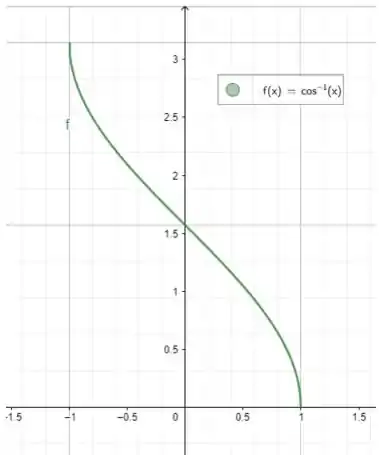
Ufa terminamos!
E é isso! Espero ter ajudado!