![]()
![]()
![]()
![]()
![]()
Passo 1
Para achar assíntotas horizontais, aplicamos o limite dessa para . Primeiro, :
Agora, :
Ou seja, temos uma assíntota horizontal para , .
Para as assíntotas verticais, devemos aplicar o limite onde a função tem descontinuidades.
No caso, a função não tem nenhum ponto descontínuo, o que significa que não temos assíntotas verticais.
Passo 2
Vamos analisar a derivada dessa função:
A exponencial é sempre positiva, então a análise de sinal pode ser feita só com o termo quadrático:
Esse cara tem pontos críticos em e em , pontos que zeram a derivada. Sendo uma parábola de concavidade negativa, vamos ter que ela é positiva entre suas raízes em e e negativa no resto do domínio.
Com isso, no ponto a derivada vai de negativa para positiva, sendo um mínimo local. No ponto a derivada vai de positiva para negativa, um máximo local.
Enfim, a função vai ser crescente de até , decrescente no resto do domínio e tem um mínimo local em e máximo local em .
Passo 3
Vamos olhar a concavidade pela derivada segunda:
Pontos de inflexão, vamos achar zerando esse polinômio:
Como essa é uma função quadrática com concavidade para cima, temos que seu sinal será negativo entre os dois pontos de inflexão, e positivo no resto do domínio.
Logo, tem dois pontos de inflexão em e em , sendo côncava para baixo entre esses pontos e para cima no resto do domínio de .
Passo 4
Esboçando, nós teremos:
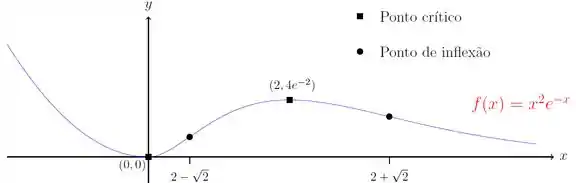
(esboço extraído do gabarito original)