Considere a função com derivadas e dadas por:
- Dê o domínio de definição de .
- Determine as assíntotas horizontais e verticais, caso existam.
- Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
- Encontre os pontos de inflexão de , se houver, e os intervalos de concavidade para cima e para baixo.
- Usando as informações anteriores, faça um esboço do gráfico de .
Passo 1
Vamos resolver letra por letra. Começando pela (a), vamos ver qual é o domínio de . Segundo o dado no enunciado, temos:
Observando a expressão, vemos que é uma razão de polinômios, ou seja, uma função racional. Funções racionais tem como domínio os números reais exceto nos pontos onde o denominador zera. Isso acontece para:
Então e não fazem parte do domínio da função:
Passo 2
Show, vamos determinar as assíntotas horizontais e verticais agora. As verticais podem acontecer nos pontos de restrição do domínio. Então, vamos testá-la para e , usando limites laterais.
O denominador está indo para zero, enquanto o numerador está indo para uma constante diferente de zero, isso fará com que o nosso limite vá para infinito. Resta saber se para mais infinito ou menos infinito.
Para isso, vamos ver os sinais:
Logo temos:
Assim:
Da mesma forma:
Como os limites vão para infinito, temos uma assíntota vertical em . Vamos testar para :
Como:
Então:
Novamente:
Assim, temos também uma assíntota vertical em . Resta calcular as assíntotas horizontais. Elas são testadas para os extremos, então temos:
Dividindo tudo pela maior potência, :
Da mesmíssima forma:
Então, também temos uma assíntota horizontal em .
Passo 3
Na letra (c), precisamos determinar os pontos críticos, os extremos relativos (máximos e mínimos) e o intervalo onde a função é crescente e decrescente.
Para isso, precisamos da derivada de , mas graças a Goku, a questão já deu:
Opa! Agora sim. Vamos começar com os pontos críticos. Eles ocorrem onde a derivada é zero ou não existe! A derivada é zero para quando . Ou seja, para . Então esses pontos serão pontos críticos.
A derivada não existe para quando o denominador zera, ocorrendo novamente em e , que também serão pontos críticos.
Vamos determinar o intervalo onde a função é crescente e decrescente, para isso, montamos uma tabelinha com os termos de e pontos críticos e analisamos o sinal:
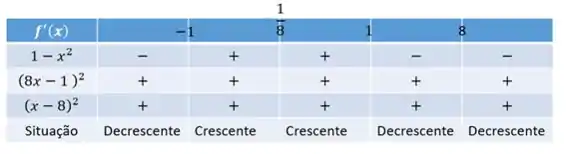
Através da tabela, também concluímos que é um ponto de mínimo, pois a derivada é negativa à esquerda e positiva à direita desse ponto. De forma contrária, dá para ver que é um ponto de máximo.
Passo 4
Para continuar, precisamos da segunda derivada, que também foi marotamente fornecida:
A concavidade é determinar pelo sinal da segunda derivada. Se positiva, é côncava para cima, se negativa, côncava para baixo.
Então vamos tentar montar uma tabela parecida com passo anterior, mas antes precisamos determinar os zeros de , que ocorrem em:
Já não possui raízes reais e é sempre positivão. Assim sendo, nossa tabela vai ficar:
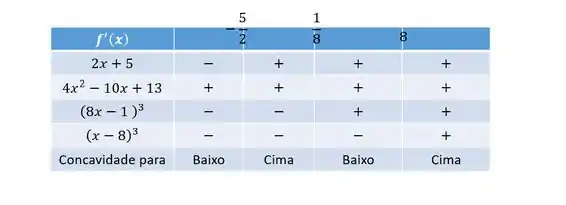
Sendo os pontos de inflexão os pontos onde a função troca de concavidade, então o ponto de inflexão será . OBS.: Apesar de os pontos e também serem pontos onde a função troca de concavidade, eles não fazem parte do domínio da função .
Passo 5
Agora, marcando as assíntotas, os pontos críticos e de inflexão, chegamos no gráfico:
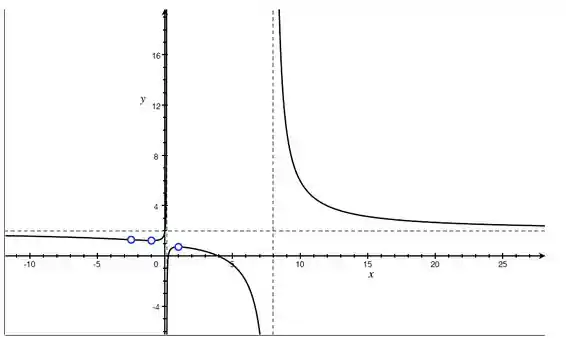
Resposta
- Assíntotas verticais:
- Pontos críticos: ; ; . Mínimo em e máximo em . Crescente para .
- Côncava para cima para .
Assíntota horizontal: