Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inequações Polinomiais

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

9. O conjunto solução da inequação 2 x 2 + 2 x - 4 x 2 - x - 2 ≤ 0 é

  1. [ - 2 , - 1 [   ∪ [ 1,2 [
  2. ] - 2 , - 1 ] ∪   ] 1,2 ]  
  3. [ - 2 , - 1   ∪ - 1,2 [    
  4. R - - 1,2
  5. ] - ∞ , - 2 ] ∪   ] - 1,1 ] ∪   ] 2 , ∞ [  

Passo 1

Oi, galerinha! Tudo bom? Aqui precisamos indicar os valores possíveis f x pode tomar, para encontrarmos o conjunto solução da inequação!

Como temos uma divisão de polinômios do segundo grau, vamos analisar o numerador e denominador em separado. Lembrando que essa divisão sempre que ser menor que um número negativo.

Bora lá!

Passo 2

Começando por,

2 x 2 + 2 x - 4

Repara que temos uma parábola com a concavidade para cima. Deste modo, o valor mínimo que f x   pode tomar é x = 0 .

f 0 = 2 0 2 + 2 0 - 4 = - 4

Agora vamos ver qual a região desta parte da função que ela continua negativa. Para isso vamos fazer f x = 0 e encontrar as raízes da equação:

2 x 2 + 2 x - 4 = 0

x 2 + x - 2 = 0

Por Bhaskara, teremos:

x = - 1 ± 1 2 - 4 1 - 2 2 1 = - 1 ± 3 2

Logo, as raízes serão

x 1 = 1

x 2 = - 2

Logo ela será negativa ou igual a zero para - 2 ≤ x ≤ 1 .

Passo 3

Já a parte

x 2 - x - 2

Repara que temos uma parábola com a concavidade para cima. Deste modo, o valor mínimo que f x   pode tomar é x = 0 .

f 0 = 0 2 + 0 - 2 = - 2

Agora vamos ver qual a região desta parte da função que ela continua negativa. Para isso vamos fazer f x = 0 e encontrar as raízes da equação:

x 2 - x - 2 = 0

Por Bhaskara, teremos:

x = 1 ± 1 2 - 4 1 - 2 2 1 = 1 ± 3 2

Logo, as raízes serão

x 1 = 2

x 2 = - 1

Logo ela será negativa ou igual a zero para - 1 ≤ x ≤ 2 .

Passo 4

Agora vamos juntar essas informações em uma tabela indicando quando o numerador e denominador são positivos ou negativos:

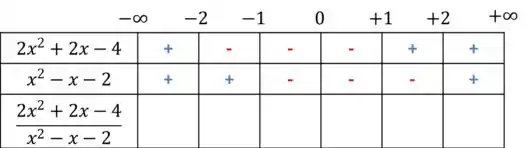
Agora vamos verificar o sinal da divisão,

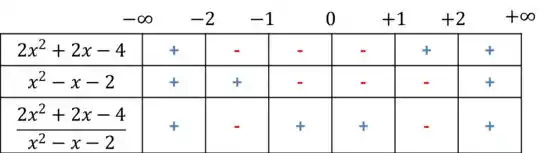
Ou seja, a nossa inequação só será 2 x 2 + 2 x - 4 x 2 - x - 2 ≤ 0 , entre - 2 e - 1 e + 1 e + 2 . Logo, o conjunto de soluções possíveis será:

[ - 2 , - 1 [   ∪ [ 1,2 [

Prontinho!

Resposta

a

Exercícios de Livros Relacionados

Use um gráfico para encontrar um número δ tal que se 5x5 + δ então x ² x - 5100 ²
Resolva a inequação.(x - 2) (x + 2)0
Estude o sinal da expressão.3 x - 1 0
Neste exercício você deverá admitir como conhecidas apenas as propriedades A 1 a ( A 4 ) , ( M 1 ) a M 4 , D , O 1 a O 4 , O A e O M . Supondo x , y reais quaisquer, prove: x ∙ 0 = 0
Estude o sinal da expressão.(2 x - 1) (x^2 + 1)