Resolva em as inequações abaixo:
- ;
- .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para resolver as seguintes inequações:
E
Uma forma de resolver é estudando os sinais delas.
E aí? Bora lá??
Passo 2
Estudando o sinal da inequação da leta a):
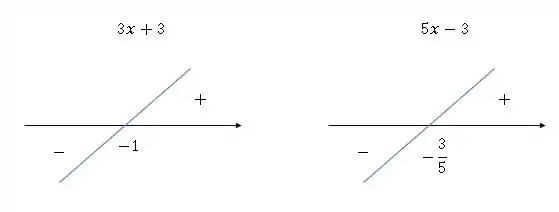
Passo 3
Nesse sentido, para que o produto seja positivo, as funções precisam possuir o mesmo sinal.
Isso ocorre em ou .
Passo 4
Estudando o sinal da inequação da leta b):
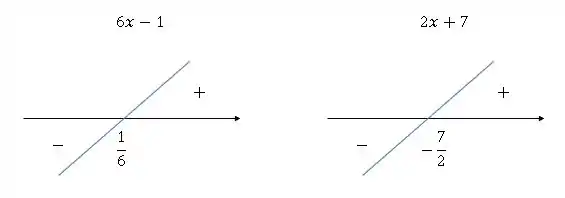
Passo 5
Nesse sentido, para que o produto seja positivo, as funções precisam possuir o mesmo sinal.
Isso ocorre em ou .
Entendeu direitinho? Responde aee ;)

Resposta
- ou
- ou