Resolva a desigualdade . Encontre o conjunto solução e ilustre ele sobre a reta real.
Passo 1
Vamos lá. Pra começar, vamos ver a definição de módulo:
Como essa definição ajuda a gente? Bem, se aplicarmos ela pras funções em módulo que temos...
... conseguimos analisar o problema em três casos:
Agora conseguimos nos livrar do módulo em cada caso e ver o que a questão nos reserva! Bora lá!
Passo 2
No primeiro caso, temos . Nesse intervalo, a desigualdade vira:
Opa, resultado maluco, não? Bem, isso diz pra gente que não tem conjunto solução nesse caso. Vamos ver o próximo então! No intervalo a inequação se transporma em:
Show, e pra fechar com chave de outro vamos ver o intervalo. Nele, a inequação se transforma em:
O que também é uma verdade! A interpretação desses resultados todos é a seguinte:
O conjunto solução será então já que ele é a condição para que a inequação esteja correta! Escrevemos sobre a reta real:
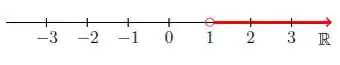
Passo 3
Na verdade mesmo já fechamos essa questão. Esse passo é só pra mostrar a interpretação gráfica dessa brincadeira. Seja:
Note pelo gráfico que só pra que teremos:
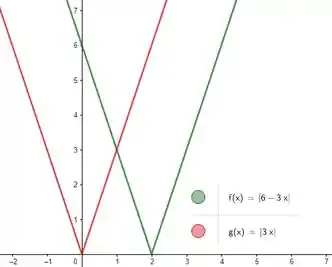
Resposta
