Resolva as inequações dos exercícios 1 a 12.
12.
Passo 1
Oi, galerinha! Tudo bom? Nessa questão, vamos resolver essa inequação de terceiro grau. Os passos são bem parecidos com o de uma equação, mas ao invés de uma igualdade, vamos ter um sinal de maior ou menor na nossa inequação.
Bora lá!
Passo 2
Temos a seguinte inequação,
Beleza, primeiramente vamos ajeitar essa inequação, jogando tudo que é para o mesmo lado sem pudor algum:
Agora temos uma inequação do terceiro grau! Bora resolver!
Passo 3
Então, galerinha, para resolver essa inequação, vamos ter que reescrever o nosso polinomio de terceiro grau.
E vamos fazer isso, aplicando o nosso famoso processo de Briot-Ruffini! Com ele conseguiremos reduzir o grau do nosso polinômio até chegar numa equação que conseguimos resolver!
Para usá-lo, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Vamos primeiro testar
Substituindo o valor, temos
Opa, essa igualdade não é verdade! . Logo, não é raíz dessa equação!
Vamos testar
Opaaaaa, com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Passo 4
Agora sim, vamos a Briot Ruffini, com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Beleza?! Então vamos lá! Arrumando o quadro, ficamos com:
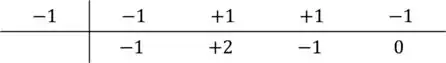
Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Essa expressão é o polinômio que estávamos procurando e podemos reescrever nossa equação como:
Portanto, nossas soluções serão:
O resultado da primeira parte, já conhecemos:
Para a segunda, como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara. Resolvendo,
Temos que
Logo:
Agora vamos fazer o estudo do sinal!
Passo 5
Então, pessoal, o que vamos fazer aqui é anisar os intervalos onde o termo é positivo e negativo.
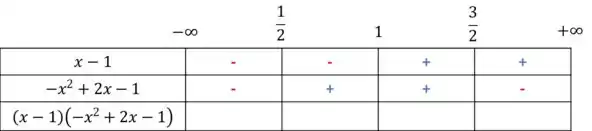
Agora, vamos fazer a multiplicação dos sinais em cada coluna, e saber o sinal é menor ou maior que zero.
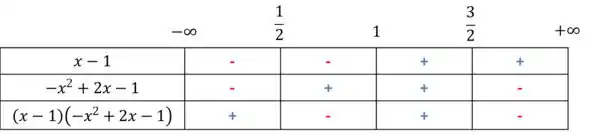
Ou seja, ela será menor que zero nos intervalos e .
A solução será, portanto: