Resolva em as inequações abaixo:
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu a inequação de segundo grau com um quociente e pediu pra gente encontrar os valores de para os quais ela está definida no conjunto dos números reais (em ).
Então, o que nós vamos fazer é encontrar as raízes de cada equação do segundo grau, pra a partir daí montar o gráfico e verificar os intervalos onde a função é negativa ou positiva.
Em seguida, nós vamos montar um quadro e fazer o estudo de sinal de cada produto e ver quais os intervalos que satisfazem a inequação, que nesse caso são os locais onde a função é positiva ou igual a zero.
Vamos lá!
Passo 2
Temos a inequação:
Pra encontrar as raízes da equação no numerador, vamos escrever:
Usando a fórmula de Bhaskara, temos:
Que nos dá as raízes:
Esboçando o gráfico dessa parábola, nós temos:
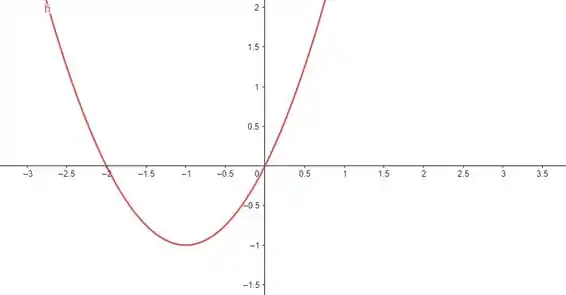
Repare que a funç��o é positiva até , que é uma de suas raízes, onde ela cruza o eixo . Depois ela passa a ser negativa, até atravessar de novo o eixo em 0, onde volta a ser positiva. Escrevendo esses dois trechos onde a função é positiva em forma de intervalo, temos:
Percebeu que nós escrevemos o intervalo fechado em e ? Isso acontece porque a nossa inequação nos diz que ela é maior ou igual a zero, então consideramos também suas raízes.
Passo 3
Pra segunda equação, que tá no denominador, temos:
Vamos encontrar as raízes usando Bhaskara novamente:
Resolvendo:
Já sabemos onde a função toca o eixo (em e ), agora vamos esboçar seu gráfico:
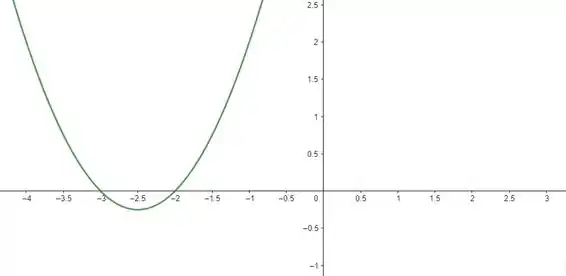
Agora vamos analisar o gráfico. Repare que aqui a função começa positiva até cortar o eixo em . Aí, ela passa a ser negativa até cortar o eixo novamente em . Depois de , a função volta a ser positiva.
Então, o intervalo onde nossa função é positiva vai ser a união desses dois intervalos. Só que agora esse intervalo vai ser aberto dos dois lados, porque o denominador de uma fração nunca pode ser zero, então não podemos considerar os zeros da função, beleza?
E aí fica assim:
Passo 4
Beleza, agora vamos analisar como fica o quociente dessas duas funções, que é a nossa inequação:
Vamos pegar os intervalos e que nós encontramos nos passos anteriores e montar a nossa tabelinha para estudar os sinais:
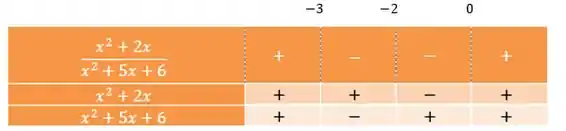
Como a inequação nos diz que o quociente maior ou igual a zero, vamos selecionar os intervalos onde o sinal é positivo (olhando pra primeira linha da tabela). Assim, o nosso conjunto solução é:
Prontinho, galera! Até a próxima! 😉