Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa função aqui
E pediu para determinarmos várias coisas! Aqui vou fazer um resumo de cada uma dessas coisas e como encontramos cada uma delas:
- Pontos críticos: pontos onde a derivada é nula
- Máximos e mínimos locais: pontos onde a derivada apresenta troca de comportamento (de positivo/negativo para negativo/positivo)
- Intervalos de crescimentos e decrescimento: crescimento – intervalo onde a derivada é positiva, decrescimento – intervalo onde a derivada é negativa
- Pontos de inflexão: onde a segunda derivada é zero
- Concavidade da função: côncava para cima – derivada segunda positiva; côncava para baixo – derivada segunda negativa;
- Assíntotas verticais: pontos em que o denominador da função é zero; Assíntotas horizontais: comportamento da função quando
Anota aí!

E é tudo isso que vamos fazer! Vamos começar analisando as assíntotas, depois analisando a derivada primeira, a derivada segunda e por fim construir esse gráfico bem bonitão!
Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Nossa função é
Existir assíntota vertical depende de termos uma descontinuidade da função. Vemos que nosso denominador tem um , e quando temos uma indeterminação! Isso significa que temos uma assíntota vertical em
Precisamos analisar a função em torno desse ponto (limite sanduíche), assim conseguimos fazer um esboço com mais clareza! Aqui é só olhar o sinal da função, aí já conseguimos descobrir se vai para ou :
 beleza?
beleza?
Para verificar assíntotas horizontais precisamos calcular o limite da função quando , beleza? Vamos começar com
Vamos aplicar a regra de L’Hopital e avaliar novamente o limite
Olhando para o temos que a função explode, então aqui não temos uma assíntota horizontal. Fazendo de forma análoga, vamos encontrar também quando , então não temos assíntotas horizontais
 bora analisar a derivada primeira?
bora analisar a derivada primeira?
Passo 3
Agora vamos analisar a derivada :
Os pontos críticos são onde a derivada é zero:
E igualando a zero temos
Achamos um ponto crítico!
Agora para classificar se é ponto de máximo ou mínimo, precisamos analisar o sinal da derivada em torno desses pontos. Se houver troca de sinal, podemos ter duas possibilidades
- De negativo para positivo: então esse ponto é de mínimo local
- Se positivo para negativo: esse é um ponto de máximo local
A ideia é testar na derivada um valor antes e um valor depois de cada ponto para saber o sinal que assume

Analisando e
Assim podemos classificar o ponto crítico:

Agora vamos ver o último quesito que envolve a derivada: intervalo de crescimento e decrescimento!
Temos que a função é crescente quando a derivada é positiva, então nesse caso
Aqui atenção: precisamos ‘quebrar’ esse intervalo em pois ali a derivada primeira não está definida. E como ali a derivada não troca de sinal, não consideramos ponto crítico

E decrescente onde ela é negativa:
Tudo bem até aqui?
Bora para a análise da derivada segunda!
Passo 4
Agora vamos analisar os aspectos que envolvem a derivada segunda! Com a derivada segunda podemos encontrar os pontos de inflexão, ou seja, os pontos onde a concavidade da função muda!
A ideia é análoga ao da derivada primeira: pegar a derivada segunda, igualar a zero e encontrar os pontos que satisfazem isso. Por fim, analisar o sinal da em torno desses pontos e encontrar a concavidade da função
- Derivada segunda positiva: função côncava para cima
- Derivada segunda negativa: função côncava para baixo
Beleza?

Vamos resgatar a derivada primeira do passo anterior:
E derivar novamente
Igualando a zero temos:
E assim temos apenas uma solução:
Isso porque o não está incluído no intervalo de definição da função, então já excluímos esse ponto!

Esse é nosso único ponto de inflexão!
Agora vamos analisar o sinal da derivada segunda não só em torno desse ponto, mas também em torno de , pois ali temos uma assíntota vertical e do passo 2 sabemos que a função se aproxima dessa assíntota por lugares diferentes! (recordar é viver: pelo lado esquerdo ela vem do , já do lado direito de , então ali a concavidade vai trocar!).
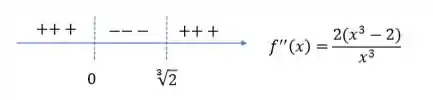
Em resumo temos
Beleza? Estamos quase lá!

Passo 5
Nosso passo final é reunir todas as informações e esboçar o gráfico da função!
E nosso gráfico ficou assim:
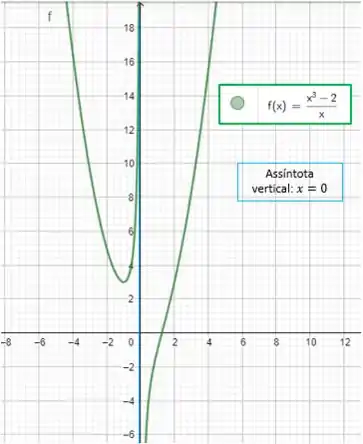
Ufa terminamos!
E é isso! Espero ter ajudado!