Considere a função , cujo domínio é o maior intervalo poss��vel para que seja inversível e para que o gráfico de (a função inversa de ) passe pelo ponto
- Determine o domíno de e de
- Determine uma expressão para
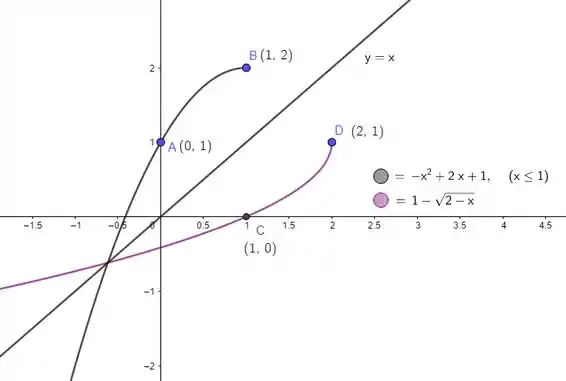
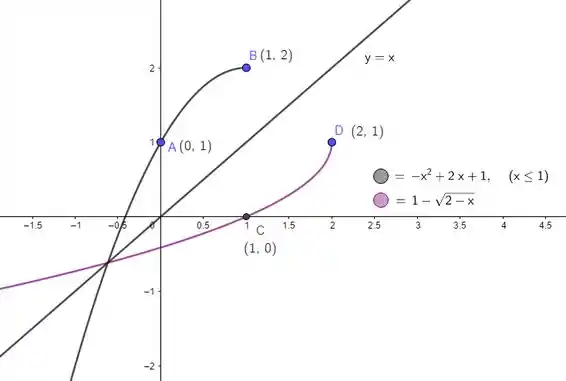
- Esboce abaixo a reta e os gráficos das funções e (em seus respectivos domínios)
Passo 1
Antes da gente começar e mergulhar de cabeça na questão, vamos dar uma lembrada rápida no conceito de função inversa:
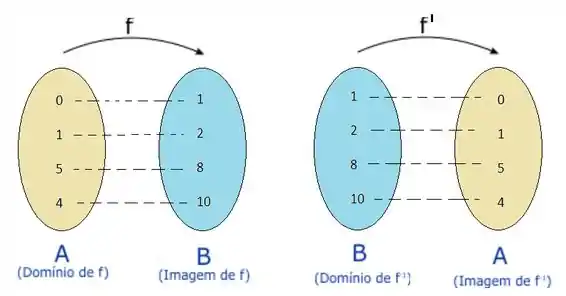
Beleza, vamos então analisar uma coisa que o enunciado nos deu o ponto . Seja:

Se pertende ao e se associa ao número , pertencente à , como:
Então pertence ao domínio de e à imagem de ! O que implica em dizer que se:
Ok, mas isso ainda não nos diz muita coisa. Vamos pensar além então. Pelo teorema da função inversa:
Bem, é um polinômio né, então é derivável pra todo . Agora, vamos ver se ta valendo. Saca só:
Se igualarmos a primeira derivada à , temos:
Opa, então não é verdade em toooodos os pontos. Mas nos domínios:
Aí sim vai ser inversível! Mas olha só! O ponto não tem que fazer parte da curva de ? Como o segundo intervalo não contém o valor , vamos ter que excluir ele! O domínimo de vai ser então:
Pra fechar a letra , vamos pegar a imagem de . Pra isso, basta substituir pelos valores extremos do domínio:
A imagem de vai ser então:
E como:
O domínio da função inversa vai ser:
Passo 2
Show, vamos achar o gráfico da inversa agora. Vamo que vamo. Seja:
Se passarmos o pro outro lado, temos:
O que ainda é um polinômio de segundo grau no qual queremos saber as raízes! Usando a querida fórmula de Bháskara:
Onde:
Ficamos com:
Ok, não acabou! Afinal, temos um sinal de ali. Como tirar ele? Bem, pra isso, vamos olhar o domínio de de novo:
Opa, então ! E se , vamos ter:
Como sempre porque temos uma raíz par, a última inequação acima só é possível se o sinal de na verdade for só um sinal de ! Show, jogamos fora o sinal de . Ficamos então com:
E agora que isolamos , podemos trocar e de lugar:
Passo 3
Última parte da questão: esboço de gráfico! No caso, a questão quer que a gente esboce não uma mas três curvas! Vamos esboçar então
Começando por , vamos fazer a primeira e a segunda derivada e igualar a , beleza? Assim a gente vai achar, respectivamente, informações sobre a inclinação da reta tangente ao gráfico e a concavidade. Derivando uma vez:
Opa, temos como ponto crítico. Vamos ver se ele é de máximo ou de mínimo ou nenhum dos dois então. Escolhendo um antes dele, por exemplo, , temos:
E escolhendo um depois, por exemplo, , temos:
Então é um ponto de máximo, o que quer dizer que antes de a função cresce e depois, decresce. Partiu checar a segunda derivada agora:
Olha só! A segunda derivada é negativa pra todo ! Então a função vai ter concavidade pra baixo o tempo todo! Juntando as informações de , e lembrando que o ponto está sobre a curva, esboçamos:
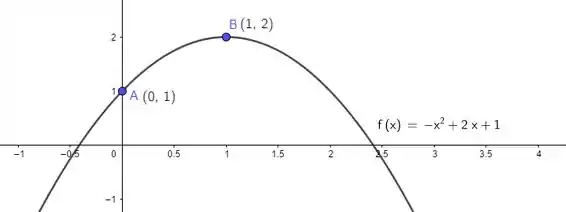
Pra segunda curva, , vamos fazer a mesmo análise, beleza? Primeira derivada primeiro então:
E veja só! A primeira derivada é sempre positiva e nunca igual à ! Ou seja, é estritamente crescente, sem pontos críticos! Agora, analisando a segunda derivada, pela regra do quociente, temos:
O que nos dá outra função no estilo da primeira derivada: sempre positiva e nunca igual à . Se a segunda derivada é assim, então tem concavidade pra cima sempre! Juntando todas as informações sobre e lembrando que pertence à curva, esboçamos:
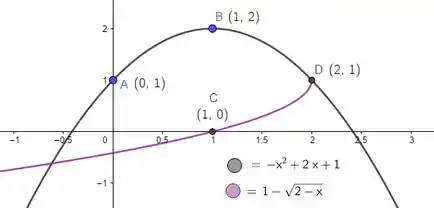
Observe que como:
Por isso que , em roxo, não tem curva para . Agora é só adicionar a curva ao esboço e aplicar os domínios das duas funções:
Como o domínio de já está representado, fechamos a questão com o esboço: