4. Considere a função cujo gráfico está representado abaixo.
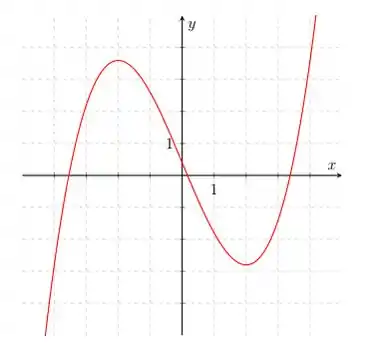
Estabeleça a ordem de crescimento dos números e .
Passo 1
Oi, galerinha! Tudo bom? Aqui temos que colocar em ordem crescente as derivadas, mas não sabemos que função é essa para poder calcular as derivadas.
Então, a solução aqui é interpretar o gráfico para estimarmos a derivada. Lembrando sempre que a derivada representava a variação ao longo do do eixo .
Deste modo, temos que:
- Se o gráfico está crescendo, ou seja, aumentando de valor conforme aumentamos nosso , a nossa derivada é positiva.
- Se o gráfico está decrescendo, diminuindo de valor conforme aumentamos nosso , a nossa derivada é negativa.
- Se o gráfico está em um pico ou vale, a derivada é nula.
Então bora lá!
Passo 2
Começando por
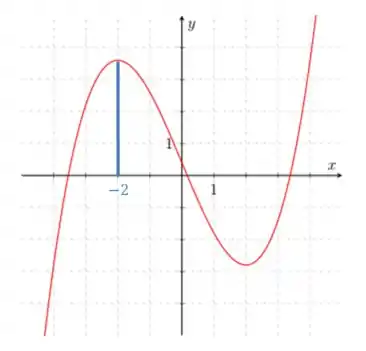
Note que estamos no cume do pico do gráfico, logo a derivada aqui é nula.
Passo 3
Para
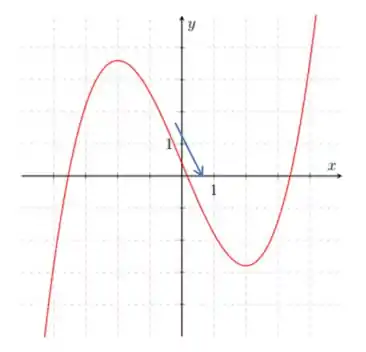
Note que a função está decrescendo, ou seja, a nossa derivada é negativa
Passo 4
Para
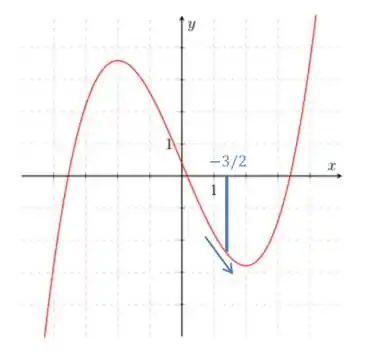
Note que a função está decrescendo, ou seja, a nossa derivada é negativa
Passo 5
Para
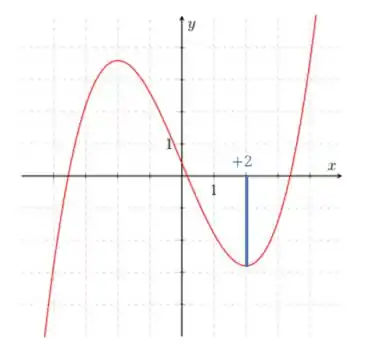
Note que a função está no vale, ou seja, a nossa derivada é nula
Passo 6
Para
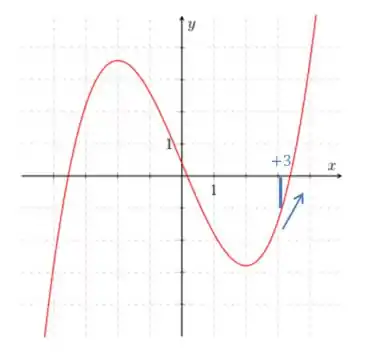
Note que a função está crescendo, ou seja, a nossa derivada é positiva
Passo 7
Organizando tudo, ficamos com
Note que a inclinação da curva no ponto é maior que no ponto , logo a sua derivada será mais negativa.