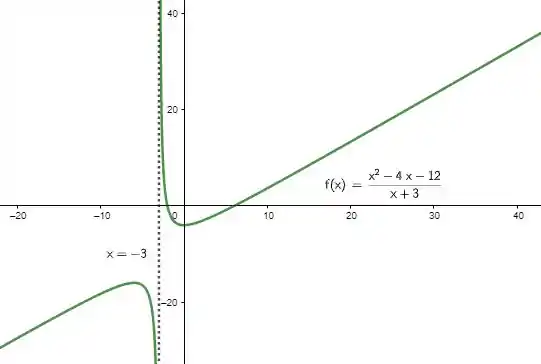
Considere a função .
- Verifique que e que .
- Ache as assíntotas horizontais e verticais caso existam.
- Identifique os intervalos onde a função é crescente e onde é decrescente.
- Encontre os valores de máximo e mínimo locais e/ou globais caso existam.
- Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão.
- Usando as informações anteriores faça um esboço do gráfico de
Passo 1
Fala povão, bora começar? O primeiro passo é confirmar pra ver se esse enunciado aí acertou as duas primeiras derivadas da nossa função. Espero que não hahaha Pra isso, vamos usar uma regra do quociente. Pra primeira derivada, temos:
E por fim, chegamos a:
A primeira então ta certa. Agora pra segunda, temos que fazer regra do quociente mais uma vez, ok? Saca só:
Dividindo tanto numerador quanto denominador por , temos:
Então beleza, o enunciado não enganou a gente, realmente temos as derivadas que ele deu!
Passo 2
Agora vamos conversar sobre assíntotas. Como a função é:
Pra gente achar assíntotas verticais, temos que fazer os limites laterais pra pontos que dão problema. No caso, o único ponto seria porque ele zera o denominador. Fazendo então:
Se pelo menos um dos limites explode, então temos sim assíntota vertical em! No caso, pra mesmo. Agora, pras horizontais, temos que fazer o limite pros infinitos. Vamos ficar com:
Ou seja, chegamos a conclusão que:
Como esses limites explodiram também pros infinitos, não vai rolar assíntota horizontal aqui. Conclusão final é:
Passo 3
Show, vamos falar sobre intervalos de crescimento, decrescimento, máximos e mínimos agora. Pra isso, vamos trazer nossa querida amiga primeira derivada de volta:
Pra analisarmos o sinal dela, vamos primeiro ver quando que ela muda de sinal. Isto é, vamos analisar os pontos críticos: Fazendo:
Vamos então analisar o sinal em intervalos que envolvam esses pontos e o ponto também, já que ele não está definido. Só cuidado que, por não estar definido, ele não pode ser um ponto de máximo ou mínimo em! Os intervalos vão ser:
Pra cada intervalo, podemos testar os valores , , e pra cada um dos intervalos, respectivamente. Vamos ter:
A partir da análise de sinais, como a função é decrescente nos intervalos em que a primeira derivada é negativa e crescente nos intervalos em que ela é positiva, chegamos a seguinte conclusão:
E como antes de a função cresce e depois decresce, esse ponto vai ser de máximo local. Analogamente, como antes de a função decresce e depois ela cresce, teremos aí um ponto de mínimo local. Não será global porque como vimos ao calcular as assíntotas, a função cresce e decresce indefinidamente nos extremos infinitos do eixo .
Passo 4
Agora pra fechar com chave de ouro vamos conversar um pouco sobre a concavidade. Pra isso, vamos analisar o sinal da segunda derivada:
Oras, essa função não zera! Galera, se uma função tem uma segunda derivada que não zera, mesmo que haja mudança de sinal, isso vai acontecer somente por causa da indefinição. Sendo assim, temos só o como ponto pra estabelecer nossos intervalos, mas não vamos ter um ponto de inflexão! Afinal, esse cara não está definido! Os intervalos no entanto, serão:
Pro primeiro, podemos testar e pro segundo, . Vamos ter:
Sendo assim, como a concavidade é pra cima quando a segunda derivada é positiva e pra baixo quando ela é negativa, vamos ter:
Perfeito! Temos tudo pra esboçar o gráfico! Juntando tudo que achamos, temos:
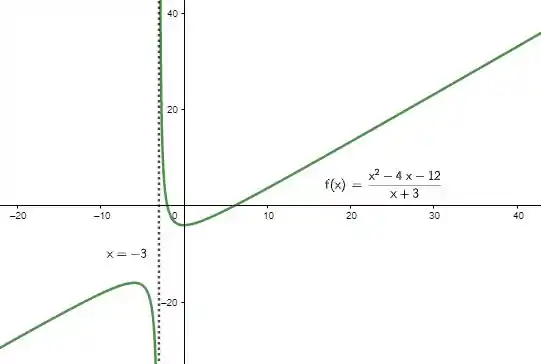
Resposta