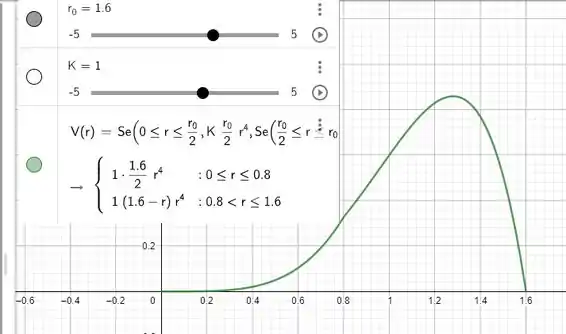
Durante o processo de tosse, provocado pela presença a traqueia de algum corpo estranho, a traqueia se contrai com o objetivo de aumentar o fluxo de ar através dela, e assim tornar mais eficiente o método de expulsão do corpo estranho. Segundo Pouseiulle, indicando por o raio da traqueia em estado normal e por o seu raio durante a tosse, o fluxo de ar na traqueia pode ser modelado por:
Onde K é uma constante positiva.
- Determine os pontos críticos de no intervalo
- Determine os intervalos de crescimento e de decrescimento de
- Determine os intervalos em que o gráfico de é côncavo para cima ou para baixo.
- Use os itens anteriores para esboçar o gráfico de no caso em que
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Quando nós tossimos, esse tossido vem muito rapido. Por que? Como dito no enunciado, é porque nossa garganta se contraio, ficando com um raio menor, assim teremos mais fluxo de ar passando por ela.
Na questão nos é pedido para determinarmos os pontos críticos dessa função do fluxo de ar, ou seja, pontos onde elas são máximas e mínimas, o que seria garganta no momento da tosse e do relaxamento, algo assim. Além disso, demais coisas sobre o gráfico da função do fluxo de ar.
Para a)
Um ponto critico é quando a derivada d função é nula. Por que nula? Porque é quando ela alcança o máximo ou o mínimo. Veja:
Assim, façamos a derivada:
Assim:
Igualando a 0:
PS: leve em conta que para primeira derivada o máximo é para , assim ao invés de podemos fazer .
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para b)
Intervalos de decrescimento são intervalo onde a função cresce ou decresce, de forma que podemos saber a partir de qual ponto ela cresce ou decresce. Para isso, basta substituirmos o ponto que achamos quando igualamos a nossa derivada da função a 0 na própria derivada da função.
“Mas por que, Mogli?” pois se a derivada da função é 0 naquele ponto, em outras palavras ela é reta horizontal, significa dizer que antes dela e depois dela a função cresce e decresce, como na imagem anterior que demos:
Repetindo a derivada:
E quando igualamos a 0, obtivemos: . Para sabermos de fato se a função cresce ou decresce naquele ponto, basta pegarmos quaisquer pontos nesse intervalo, se ela é maior que 0 significa que ela está crescendo, isso é chamado de varal de crescimento e decrescimento, e é dessa forma:
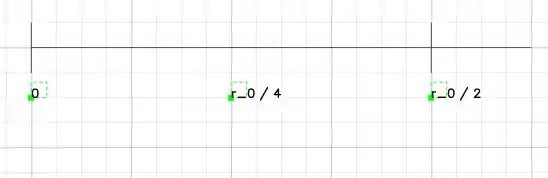
Onde escolhemos como um ponto no intervalo , e é com ele que vamos saber se a função cresce ou decresce.
Assim, aplicando na nossa derivada, temos:
pois não há como o raio de uma garganta ser menor que 0.
Assim veja que a função é intervalo de crescimento.
Agora para a outra derivada, temos:
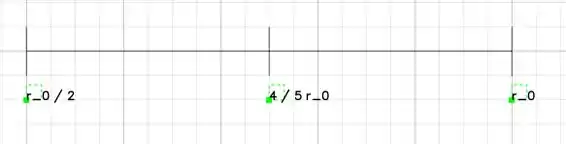
Peguemos por exemplo os pontos
Para o intervalo entre
E:
Para o intervalo .
Assim ficando no nosso varal:
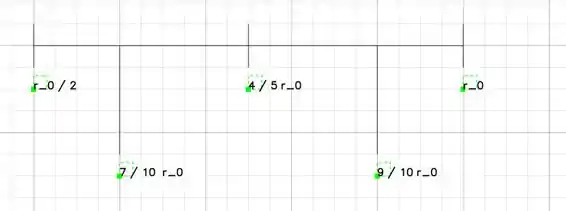
Vamos analisar para o intervalo com o ponto primeiro. Assim:
Veja que, assim:
Assim a função cresce nesse ponto.
Agora para o intervalo com o ponto :
Veja que . Assim:
Logo a função decresce nesse ponto.
Portanto, pegando os pontos de crescimento e decrescimento, temos:
Passo 3
Para c)
Para a determinação do intervalo de concavidade de uma função devemos pegar a segunda derivada igualar a 0 e verificar se ela é positiva ou negativa. Para melhor visualização, veja essa imagem:
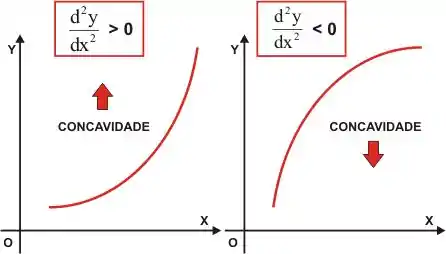
Ficou mais claro, né carinha?!
É parecido com o item anterior, não é?!
Sendo assim, derivemos a nossa função derivada de , ou seja:
Ficando:
Igualando a 0, temos:
Aplicando o mesmo varal que usamos no interior, sob os mesmos intervalos, temos:
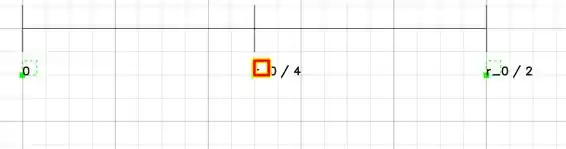
Com o ponto
Temos:
Veja que , assim a função nesse intervalo tem concavidade para cima.
Para o outro pedaço da função:
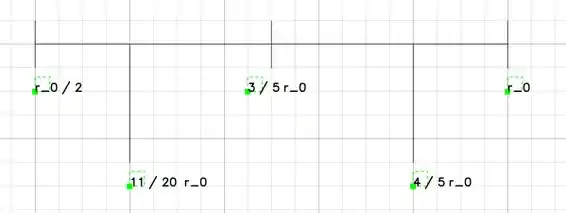
Veja que pegamos o ponto para analisarmos entre o intervalo , e para analisarmos entre intervalo . Assim, bora lá analisar?
Fatorando , temos:
Assim, por ser positiva, a função nesse intervalo, de , tem concavidade positiva.
Para o outro lado do intervalo, com para o intervalo , temos:
Fatorando , temos:
]
Veja que , assim:
E assim, por ser negativa, a função tem concavidade para baixo.
Resumindo:
Passo 4
Com isso tudo já definido, podemos montar nosso gráfico seguindo os passos dados nos itens anteriores.
Ficando algo assim nessa pegada;
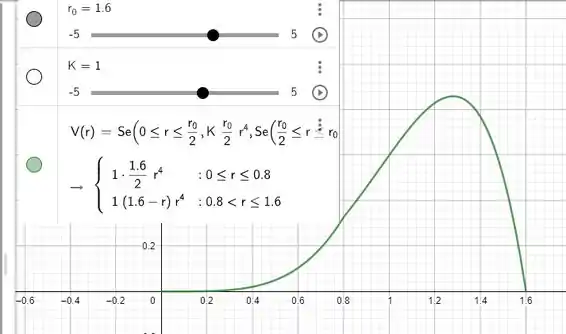
Resposta
Para a)
Para b)
Para c)
Para d)