2) Esboce o gráfico de

Considerando: domínio, interseções com os eixos, limites necessários, regiões de crescimento e decrescimento, máximos e mínimos, regiões de concavidade e pontos de inflexão.

Começando pelo domínio.

Como a função possui , precisamos observar o seguinte:

Essa é uma função definida no intervalo , lembrando que zero não está no intervalo. Portanto não há valores negativos possíveis assim como o zero.

Portanto o domínio é:

Nesse passo, falaremos sobre a interseção com o eixo .

Mais uma vez, observaremos a função :

Essa função tem valores negativos no intervalo , lembrando que esse intervalo não engloba , já que .

Levando esse intervalo em conta, vamos pegar dois valores bem próximos dos limites e ver o que acontece com nossa função:

Primeiro, :

Concluímos que o gráfico corta o eixo a primeira vez em uma região bem próxima de e assume valores de negativo.

Agora, :

Concluímos que o gráfico corta o eixo pela segunda vez em uma região onde .

O próximo item é o limite. Olhando para o nosso domínio, vemos o infinito positivo para a direita e intervalo aberto em a esquerda. Esse intervalo aberto em é um ponto possível de assíntota. Vamos verificar?

Esse limite pela direita é uma assíntota vertical no nosso gráfico. Essa informação é importantíssima para a construção do gráfico.

Encontraremos agora o ponto de máxima/mínima.

Para isso, precisamos derivar a função:

Obs.: Derivamos utilizando pela regra da cadeia.

Agora, vamos igualar essa derivada a :

Essa é a coordenada do ponto que estamos procurando.

Aplicando na função original:

Pronto, conhecemos o ponto:

Para sabermos se é de máxima ou de mínimo, vamos avaliar a segunda derivada de :

Como a segunda derivada retornou um valor positivo, esse ponto é de mínimo.

Agora que temos todas essas informações, podemos traçar o gráfico:

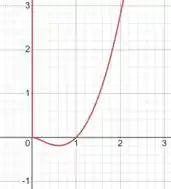
Ufa! Terminamos!

Pra essa questão é isso pessoal! Bora pra mais uma?