Esboce o gráfico da função
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Nessas questões de gráficos vamos precisar seguir um roteiro que temos lá no nosso conteúdo sobre esboço de gráfico. Eu não vou colocar ele aqui no passo (1), porque senão vai ficar muito poluído e assim, tem bastante passos, e poderia assustar vocês de início. Mas, como eu tô aqui pra mostrar pra vocês que é super tranquilo de se fazer, vamos seguir naturalmente!!
Mas eu recomendo que você depois de fazer essa questão comigo, vá lá no nosso conteúdo e escreva esse roteiro no seu coração porque vai te ajudar muitooooo!!!
Passo 2
O primeiro passo é a gente descobrir nosso domínio, ou seja, quando essa função existe e não vai dar problema. Perceba que ela é uma função polinomial e que tem divisão no denominador, e aqui a gente tem que sempre prestar atenção, porque toda vez que uma função for uma razão de funções, tem que ficar ligado se vai ter problema no denominador.
Note que não importa o valor que coloque pra , o denominador SEMPRE será maior que 1. E em cima, pode assumir qualquer valor, logo, isso implica dizer que nosso domínio são todos os reais!!
Passo 3
Vamos ver agora as intersecções dos eixos. COMO EU FAÇO ISSO?!
Toda vez que você quiser saber intersecções de eixos, basta você zerar e ver quanto dá e vice-versa. Se liga!!
Que é a mesma coisa que escrever:
Para temos
E quando , temos
Ou seja, as intersecções com os eixos e são ambos 0.
Passo 4
Uma malandragem agora é a gente verificar se essa função é ímpar ou par. Se ela for ímpar, nossa função será simétrica em relação à origem, o que é ótimo, porque poderíamos restringir nosso domínio de análise de 0 até infinito e depois só rebater no outro sentido.
Para saber se é ímpar, precisamos verificar se , então bora testar!!!
Opaaaa! Nossa função é ímpar!!
Passo 5
Vamos agora avaliar as assíntotas verticais e horizontais!
Uma outra malandragem aqui é: toda vez que a denominador de uma função NUNCA PODER DAR ZERO, isso indica que é uma assíntota vertical. Agora vamos ver o que acontece quando fazemos .
quando
quando
Opa, uma vez que isso aí de cima é verdade, não há assíntotas horizontais.
Passo 6
Agora vamos precisar da primeira e segunda derivada da nossa função porque vamos ver questões de concavidades e pontos de inflexão. Para te lembrar, ponto de inflexão é aquele ponto quando a nossa curva está crescendo antes dele e depois está decrescendo ou vice-versa, o importante é lembrar que nossa curva vai mudar o sentindo (crescente ou decrescente) depois desse ponto.
Vamos aplicar a regra do produto aqui, beleza?
Uma vez que , para todo com exceção de , é crescente em .
Embora , não muda o sinal em , logo não há máximo ou mínimo local.
Passo 7
Agora vamos avaliar a derivada segunda e ver o lance dos pontos de inflexão!!!
Agora, vamos precisar pegar as raízes dessa derivada segunda e fazer uma tabela de acordo com os intervalos dessas raízes. Para fazer isso, basta igualarmos a zero!!
Note também que zera nossa , portanto também é uma raiz dessa equação.
Vamos montar a tabela!!!

Os números críticos que gerarão nossos pontos de inflexão são aqueles quando nosso sinal mudar na . Ou seja, temos três números que farão isso, né?
Pegando esses valores e substituindo na , vamos descobrir quais são os valores de para montarmos quais são finalmente os pontos de inflexão. Portanto, os pontos de inflexão são .
Passo 8
Portanto, o gráfico finalmente pode ser construído como o abaixo:
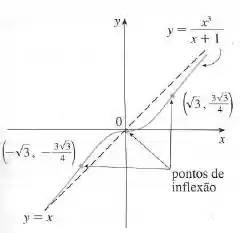
Uffa!! Deu trabalho, mas valeu a pena né?
Te espero na próxima questão!!
