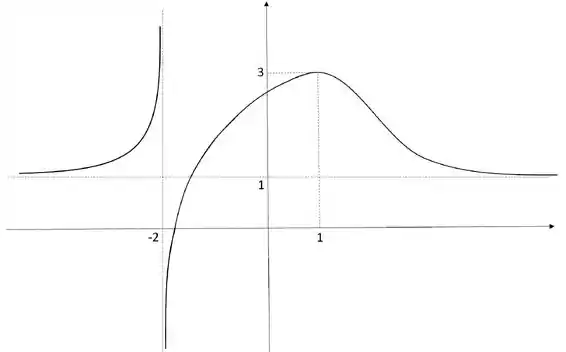
3) Esboce o gráfico de uma função que satisfaça as seguintes condições:

• é contínua em todo o seu domínio
• é crescente nos intervalos e
• é decrescente no intervalo

Passo 1

Essa questão facilita a nossa vida no esboço porque ela nos dá tudo, viu? Só vamos precisar interpretar direitinho. Então bora lá. Vamos começar com o domínio:

Veja então que a função está definida para qualquer real menos . Graficamente, isso quer dizer duas coisas:



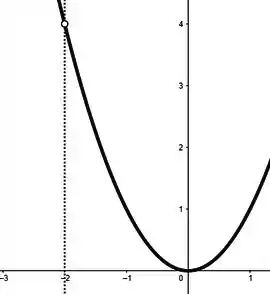
Ou a função tem essa cara e simplesmente não está definido...



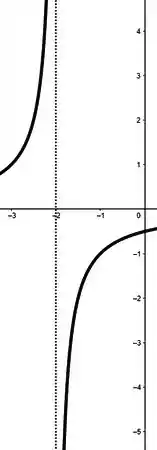
...ou é uma assíntota vertical! Já deu pra ver que vamos precisar ficar de olho nas assíntotas né? Então vamos buscar elas

Passo 2

Beleza. Pra buscar assíntotas, temos que lembrar que precisamos fazer limites. Então vou trazer de volta alguns dos limites do enunciado.

Mas porque estamos olhando só pra esses dois? Porque, veja bem, em uma função sem assíntotas nenhuma, nem vertical nem horizontal, seja pertencente ao domínio de :

Agora, se existem assíntotas verticais, o limite para tendendo ao número, vai ser infinito ou menos infinito e se existem assíntotas horizontais, o limite pros infinitos serão números. Show, se:

Então de fato:

E veja bem, se se aproxima de pela esquerda (valores menores que ), o limite é diferente do se aproximando pela direita (valores maiores). Sendo a função ainda, segundo o enunciado, crescente nos intervalos e , acaba que, graficamente, temos algo semelhante à:



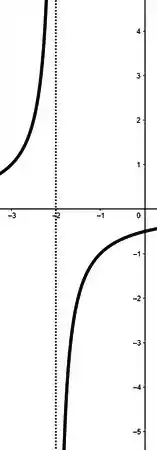
Show, agora vamos ver as assíntotas horizontais. Temos sim informações sobre elas ó:

Maravilha, nossa única assíntota horizontal vai ser então:

E usando essas informações, já da pra fazer um pré esboço:



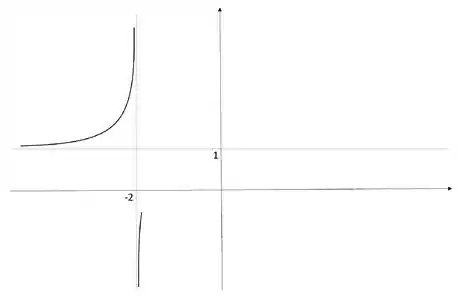
Passo 3

Ok, mas não sentiu falta de um limite não? O que faremos com esse aqui:

A primeira coisa que podemos notar nesse limite, é que se pertence ao domínio de , então:

Opa, não é que o limite que faltou se encaixa nesse modelo? Podemos afirmar então que:

É um ponto da nossa curva. Vamos marcar ele então no nosso esboço:



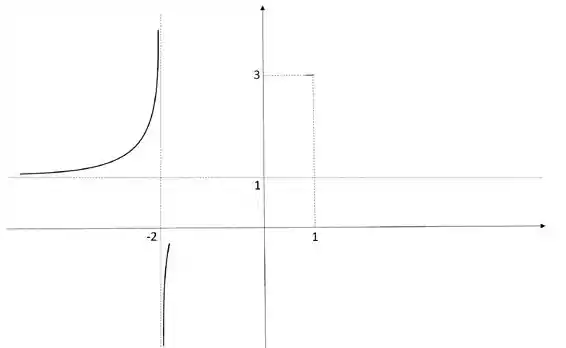
Passo 4

Pra fechar, vamos olhar pras informações sobre intervalo de crescimento e decrescimento

• é crescente nos intervalos e
• é decrescente no intervalo

Ou seja, saindo de a função tem que crescer até alcançar o ponto que a gente já sabe que ele passa:

O esboço vai ficar:

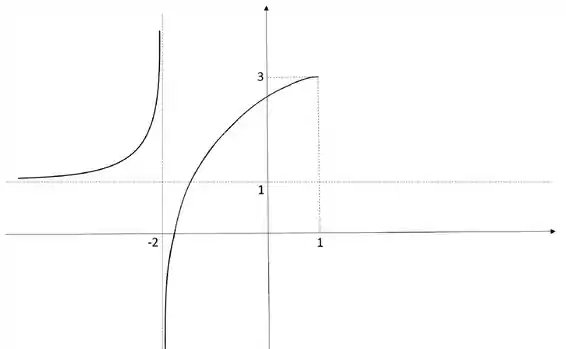
E depois desse ponto, como a função decresce, traçamos uma linha até , assíntota horizontal, mas sem nunca tocar nela, ok?

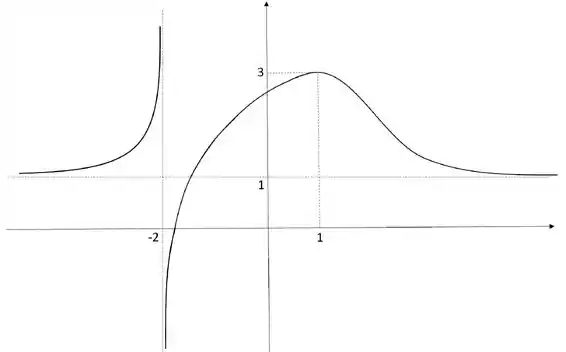
E taí! Questão finalizadíssima. Agora é só partir pro abraço.

Resposta