Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-

cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso

existam).

Primeiramente, vamos calcular a derivada da função f(x). Como a derivada de uma soma de funções é simplesmente a soma das derivadas. obtemos

Igualando a derivada a zero, obtemos os pontos de extremo

Resolvendo a equação de segundo grau, obtemos as raízes e . Então, já sabemos que nesses pontos, a função f(x) tem dois extremos. Agora só precisamos saber qual dos pontos é um máximo e qual é um mínimo. Para isso vamos calcular a concavidade da função, através de sua derivda segunda. Derivando a expressão obtida para a derivada primeira, obtemos

Dessa expressão, vemos que para , a função é positiva porque

Portanto, a raiz é um ponto de mínimo, pois é um extremo com concavidade positiva. Semelhantemente, a derivada segunda é negativa quando

O que caracteriza como um ponto de máximo, pois é um ponto de extremo com concavidade negativa. Além disso, descobrimos também que a função tem um ponto de inflexão em x = 2, pois é quando sua derivada segunda é nula e, a partir do qual, o sinal da concavidade se inverte.

Agora, devemos estudar o comportamento da função quando fazemos x vai à ou . Quando , temos

Como o termo cúbico cresce mais rapidamente que os outros polinômios, temos que a função decresce infinitamente quando x tende à , por ser um polinômio de ordem ímpar, mantendo assim o sinal negativo. Semelhantemente, pelo mesmo argumento, quando temos

Então, temos uma função que é infinitamente negativa quando , cresce conforme aumentamos x e com concavidade negativa até que atinge um máximo em , a partir de onde começa a decrescer, até atingir o ponto de inflexão . A partir daí a concavidade é positiva e a função atinge um mínimo em . Conforme aumentamos x, a função cresce indefinidamente, como constatado no último limite. Dá uma olhada no gráfico da função: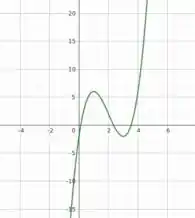

A questão foi isso! Te vejo na próxima! Tchau Tchau!