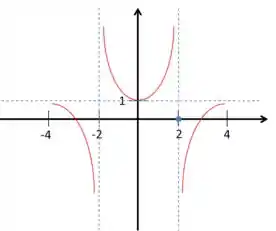
3. Uma função satisfaz as seguintes propriedades:
- e
- é estritamente crescente em e
- é uma função par
- Esboce o gráfico de uma tal função.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que esboçar o gráfico de uma função desconhecida, baseado em algumas informações que foram nos passadas.
Então vamos interpretando cada informação e montando o gráfico.
Bora lá!
Passo 2
A primeira informação é , ou seja, a função passa pelo ponto .
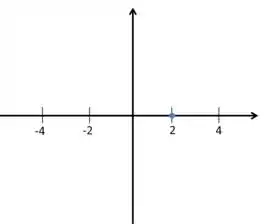
Passo 3
Agora vamos olhar para a seguinte informação:
e
Repara que quando tende a tanto pela esquerda, como pela direita, a nossa função vai para o infinito (positivo e negativo). Ou, seja, ali temos uma assíntota.
Juntando essa informação o fato de que ela é estritamente crescente em e , podemos montar:
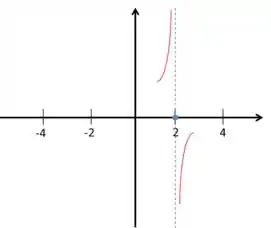
Passo 4
Buscando agora as assíntotas horizontais, vamos olhar para essa informação
Ou seja, temos uma assíntota horizontal em .
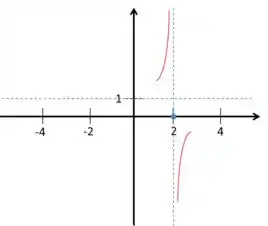
Mas repara que também temos que,
Logo, temos o ponto ,
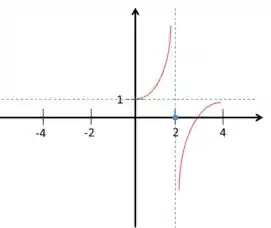
Passo 5
Por fim, vamos usar a informação de que temos uma função par. Ou seja, podemos espelhar o lado positivo, no lado negativo. Fica assim:
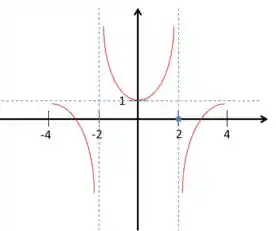
Resposta