Seja f: ⵏR ⟶ ⵏR definida por .
(a) Esboce o gráfico de ?
Passo 1
Eaew, tudo certinho contigo?
Temos que esboçar o gráfico de .
Vamos fazer isso, vem comigo!
Passo 2
Primeiro temos que encontrar os intervalos. Temos que
, equivale ao intervalo
, equivale a e
então,
, se ;
, se e .
Passo 3
Agora podemos esboçar o gráfico dessa função
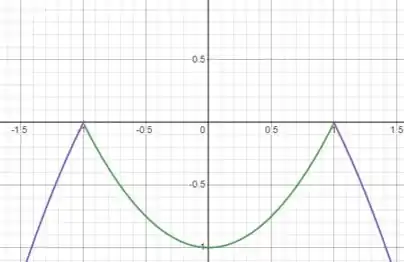
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo da questão.