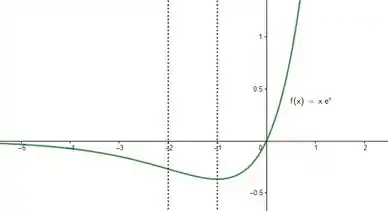
Seja .
- Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo
- Determine os intervalos onde é côncava pra cima/baixo e os seus pontos de inflexão
- Caso existam, encontre as assíntotas horizontais e verticais de
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens e
Passo 1
Bora começar então! Pô, indo na ordem do enunciado, a primeira coisa que temos que fazer é conversar sobre intervalos de crescimento e decrescimento. Pra isso, vamos precisar do sinal da primeira derivada! Partiu então, usando uma regra do produto, achamos:
Show de bola! Agora pra analisar o sinal, vamos ver primeiro quando que a primeira derivada zera:
O truque vai ser analisar então o sinal da derivada em intervalos que envolvam o ponto encontrado acima. Já que só achamos um ponto crítico os intervalos vão ser:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Opa, então a função decrescia antes de chegar em (porque a primeira derivada é negativa) e depois passou a crescer (porque a primeira derivada se tornou positiva). Isso quer dizer então que o ponto que achamos é um ponto de mínimo! Resumindo tudo bonitinho fica assim:
Passo 2
Maravilha, agora a gente vai continuar fazendo uma análise beeeeem semelhante a anterior, só que dessa vez pra segunda derivada, tranquilo? Vamos ter:
Como essa derivada que sobrou nós já fizemos...
Tranquilo! Agora analisando o sinal, vamos ver quando que a segunda derivada zera:
O truque vai ser analisar então o sinal da derivada em intervalos que envolvam o ponto encontrado acima. Já que só achamos um só o , os intervalos vão ser:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Opa, então a função tinha concavidade pra baixo antes de chegar em (porque a segunda derivada é negativa) e depois passou a ter concavidade pra cima (porque a segunda derivada se tornou positiva). Isso quer dizer então que o ponto que achamos é um ponto de inflexão! Resumindo tudo bonitinho fica assim:
Passo 3
Calma que ta acabando galera, última coisa antes do esboço e do abraço! A questão quer as assíntotas, né não? Felizmente nesse caso só vamos precisar nos preocupar com as horizontais. Porque? Bem, dá uma olhada na função:
Será que tem algum valor de que se eu der pra minha função ela não consegue me retornar um número? Pô, acho que não em! Se não existem restrições pra função, ou seja, se o domínio dela é o próprio conjunto dos reais, não temos candidatos a assíntotas verticais! Agora, pras horizontais, fazemos:
Temos sim uma assíntota! A horizontal (ou o próprio eixo , pros íntimos)
Passo 4
Juntando tudo, conseguimos partir pro abraço esboçando esse carinha aí!
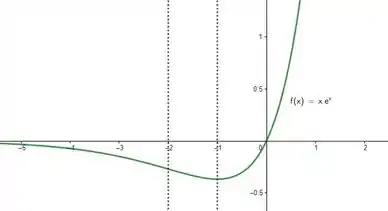
Resposta