Seja
(e) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c), justificando.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o gráfico da função usando as informações dos itens anteriores.
Bom, nós já determinamos os intervalos de crescimento e decrescimento da função, seus pontos de inflexão, intervalos onde a função é côncava para cima e para baixo e suas assíntotas horizontais e verticais. Então, juntar tudo e colocar isso no plano cartesiano.
Vamos lá!
Passo 2
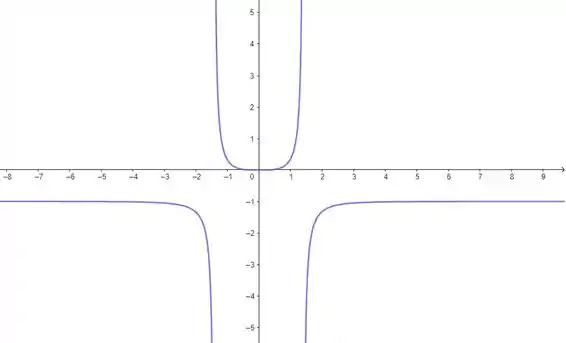
No item (a), nós vimos que a nossa função não apresenta pontos de máximo e mínimo definidos, mas tem um ponto de inflexão em . Vimos também que a função cresce no intervalo e decresce no intervalo .
No item (b), nós vimos que a função tem concavidade para cima nos intervalos e que tem concavidade para baixo no conjunto , e fizemos esses testes analisando o sinal da derivada segunda, lembra?
Por fim, no item (c), nós encontramos uma assíntota horizontal em , calculando os limites para . E também encontramos duas assíntotas verticais em e .
Usando essas informações, nós conseguimos plotar o gráfico de :
Valeu, galera! Até a próxima! 😉