Seja duas vezes diferenciável e tal que
• , e
•, , ,
• se e se
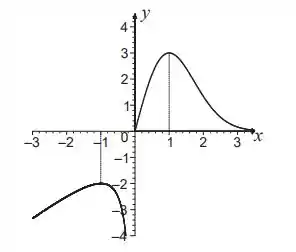
• o gráfico de está dado abaixo
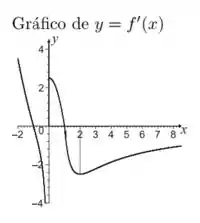
Nestas condições,
(a) prove que
(b) prove que
(c) esboce um possível gráfico de
Passo 1
Organizando as informações dadas no enunciado, podemos fazer o seguinte quadro:
![]()
Além disso, podemos concluir que se existe e para qualquer , então é contínua para todo . Logo, seu domínio é
Passo 2
(a) Pelo quadro, podemos afirmar que é crescente no intervalo e positiva em , pois . Como
significa que à medida que se aproxima de zero pela direita, o valor da função se aproxima de zero também. Já que , os valores da função irão diminuir de até próximo de quando for se aproximando de zero pela direita. Com isso, podemos afirmar que no intervalo .
Agora precisamos provar que no intervalo , porque assim, consequentemente, provaremos que para todo valor de maior que zero.
Pelo quadro, temos que
Então, quando cresce infinitamente a partir de , a função irá de para valores positivos muito próximos de zero.
Assim, com certeza podemos afirmar que
Passo 3
(b) Pelo quadro, podemos afirmar que é crescente no intervalo e negativa em , pois . Como
significa que, a partir de , à medida que tende a , o valor da função vai de até . Por isso, podemos afirmar que no intervalo a função é negativa.
Já no intervalo , como e
significa que o valor da função irá decrescer de até .
Assim, provamos que
Passo 4
(c) A partir das informações do enunciado e do que descobrimos nos itens anteriores, podemos faze as seguintes afirmações:
- é um máximo relativo, pois, nesse ponto, o sinal da derivada muda de positivo para negativo
- é uma assíntota vertical, pois
- é um máximo relativo, pois, nesse ponto, o sinal da derivada muda de positivo para negativo
- A função é côncava para baixo no intervalo , pois se e
- A função é côncava para cima no intervalo , pois se
- é ponto de inflexão
Agora podemos esboçar o gráfico, que fica assim: