UFRJ – Cálculo 1 – Lista 12 – Questão 3b
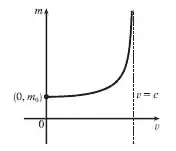
Na teoria da relatividade, a massa de uma partícula é
Em que é a massa de repouso da partícula, é a massa quando a partícula se move com velocidade em relação ao observador e é a velocidade da luz. Esboce o gráfico de como uma função .
Passo 1
Bom galera, nesse exercício estamos interessados em esboçar o gráfico da variação da massa de uma partícula em função da sua velocidade. Para isso iremos utilizar os conceitos de assíntotas, máximo e mínimo local, ponto de inflexão, crescimento e decrescimento e concavidade.
Passo 2
Primeiramente iremos encontrar a interseção de com os eixos. A interseção com o eixo vertical é
Não há interseção com o eixo horizontal . Dessa forma, podemos encontrar as assíntotas resolvendo o seguinte limite
Dessa forma, em temos uma assíntota vertical.
Passo 3
Derivando nossa função em relação a , temos
Como , então está crescendo em . Não existem pontos de máximo nem mínimo locais.
Derivando , temos
Como , então possui concavidade para cima em . Não existem pontos de inflexão na função.
Resposta
