Ar úmido a , ede umidade relativa e resfriado a uma pressão constante ate a temperatura do ponto de orvalho. Determine o resfriamento (em de ar seco) necessário para esse processo.
Passo 1
Precisamos determinar o resfriamento deste processo sobe pressão constante.
Temos que assumir que o processo está em regime permanente.
O fluxo de massa permanecera constante pelo processo todo pela lei da conservação da massa.
A variação da energia cinética e potencial é insignificante.
Sabemos que a umidade no ar é constante .
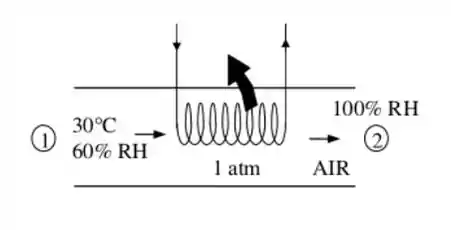
As propriedades de entrada pode ser determinadas pelo diagrama piscométrico do gráfico e figura A-31.
Propriedades de entrada:
Propriedades de saída:
E por estas condições de saída temos:
Passo 2
Utilizando o balanço de energia no ar, o resfriamento é determinado por: