Funções Vetoriais

Aqui nessa página nós temos o intuito de fazer uma introdução sobre as funções vetoriais para que você possa ter uma noção inicial desse assunto antes de se aprofundar. Então bora lá!

O que são Funções Vetoriais?

Vamos começar entendendo o que são funções vetoriais.

Você lembra que a gente pode representar um vetor indicando sua direção pelas coordenadas e ?

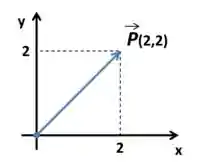
Quando essas corrdenadas, e , de um vetor forem dadas por um função, dizemos que essa função é uma função vetorial.

Essa funções vetoriais podem ser de , , , ou várias variáveis.

Vamos pegar um exemplo de função vetorial de três variáveis:

O que temos aqui é que a função tem três variáveis independentes (, e ) e ela pega essas três variáveis e leva elas a vetores com apenas duas corrdenadas, e , sendo a coordenada dada por e a coordenada por .

Vamos pegar o ponto . Se aplicarmos a função nesse ponto, teremos como resultado um vetor que será:

Sacou?

Domínio de Funções Vetoriais

O domínio de funções em geral é o conjunto de valores das variáveis independentes no qual a função está bem definida. Aqui nas funções vetoriais não é diferente, preisamos analisar todas as variáveis independentes envolvidas e ver em qual conjunto delas a função vetorial está bem definida.

Lembrando dos seguintes pontos para encontrar domínio:

• Nas frações, o denominador não pode se zero;
• Dentro das raízes quadradas não pode ter número negativo;
• O valor dentro do logaritmo tem que ser positivo.

Vamos ver um exemplo aqui:

Temos a função, que podemos chamar de , que descreve a primeira coordenada do vetor, e temos a função , que descreve a segunda coordenada do vetor:

Olhando para vemos que não tem nenhuma restrição, tanto quanto podem assumir qualquer valor.

Agora olhando para , como temos uma raíz quadrada, precisamos garantir que o valor no interior da raíz seja positivo:

Então, temos que o domínio será:

Imagem de Funções Vetoriais

A imagem será o conjunto dos possíveis valores que são obtidos ao substituir as variáveis por um número na função.

Para uma função vetorial, a imagem normalmente será uma superfície e para encontrarmos essa superfície temos que achar uma relação entre as componentes do vetor que compõe a imagem.

Vamos no exemplo que fica mais tranquilo:

Se chamarmos a terceira componente de , temos:

Essa expessão é a nossa relação entre as componentes do vetor, e essa relação define a parte de cima de um cone. Então, todos os vetores obtidos por essa função estarão contidos nessa parte do cima do cone:

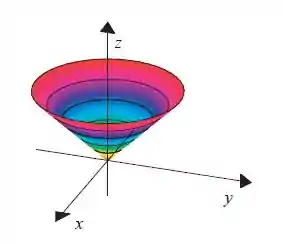
Bem irado não é?

Era isso que tínhamos para falar pra você nessa introdução de funções vetoriais. Se você quiser, pode conferir esse mesmo conteúdo de introdução em vídeo 👇🏽. É bom pra fixar bem hahaha

Agora que já viu essa introdução fica bem mais fácil continuar explorando esse assunto. E fica ainda mais fácil com o Responde Aí, porque separamos todo o conteúdo que você precisa saber sobre funções vetoriais em capítulos e tópicos pra você estudar de maneira bem lógica e rápida. Confere nosso Raio-X aqui em baixo e veja tudo que temos para te oferecer 👇🏽