Dinâmica de Rotações

Fala ai! Bem vindo ao RespondeAí, nessa página você vai conhecer tudo que abordamos no nosso assunto de Dinâmica de Rotações!

Definição

Em dinâmica de rotações estudamos o movimento dos corpos que giram ao redor de algum ponto, que chamamos de eixo de rotação, por exemplo a terra gira entorno do sol, então o sol representa um eixo de rotação para a terra.

Momento Linear

Quando uma partícula entra em movimento de rotação, podemos definir o momento de inércia dessa partícula a partir da fórmula do momento de inércia:

Onde:

• é o momento de inércia da partícula, medida em
• é a massa da partícula, medida em
• é a distância da partícula até o eixo de rotação, medido em

Na figura abaixo temos um exemplo de um sistema com duas partículas:

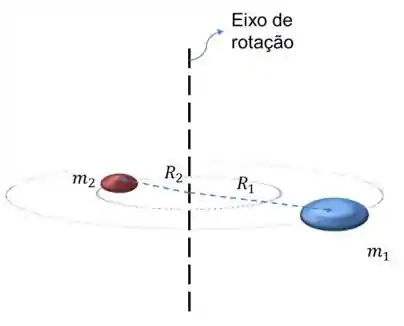
Podemos dizer que o momento de inércia do sistema vale:

Torque

Além disso sabemos que um corpo em rotação possui um certo Torque associado ao seu movimento, e podemos calcular o torque associado ao movimento do corpo a partir do produto vetorial:

Se pararmos para analisar essa fórmula, quanto maior o raio de rotação, maior vai ser a facilidade com que uma força vai conseguir gerar torque em um objeto, por isso as maçanetas das portas ficam do lado oposto da porta ao eixo de rotação da porta, diminuindo assim o esforço necessário para abrir ou fechar a porta.

Também podemos encontrar o módulo do toque a partir do momento de inércia do objeto, com a seguinte fórmula:

Onde é a aceleração angular do objeto.

E a gente deve sempre lembrar a relação entre aceleração tangencial e aceleração angular:

Show! Já falamos de dois conceitos super importantes, então agora vem comigo e confere aqui em baixo nosso RAIO-X com todos os capítulos e tópicos que abordamos no assunto de Dinâmica de Rotação.

Você ainda tem muito o que aprender sobre Teorema dos Eixos Paralelos, Polias Não-Ideais, Rolamento sem Deslizamento, Momento Angular e Colisões com Rotações e esses são só alguns dos tópico veremos em seguida!

Aproveite e aprenda um pouco mais sobre a Regra da Mão Direita e sobre o torque, conferindo esse exercício resolvido em vídeo com nossa solução Passo a Passo desenvolvida pelos nossos Experts, para fazer você mandar bem em dinâmica das rotações: