Matrizes e Sistemas Lineares

Fala aí galera linda, tudo bem com vocês? Nós somos o Responde Aí, a plataforma de exatas que veio pra salvar o seu semestre!

Hoje nós vamos falar aqui sobre Matrizes e Sistemas Lineares!

Sistemas lineares são conjuntos de duas ou mais equações, com duas ou mais incógnitas, nas quais só estão envolvidas operações básicas como soma, subtração, divisão e multiplicação.

E qual a relação entre Sistemas lineares e Matrizes?!

Podemos escrever os sistemas lineares em forma matricial 😱😱😱 E isso vai ser um super adianto para resolver os sistemas lineares! 🤩🤩🤩

Então sem mais enrolo, confere esse videozinho que eu separei pra você!

Ou se você preferir, temos um resumo em texto! Confere aqui em baixo 👇👇👇

Como escrever um sistema linear em matriz?

Se liga no sistema linear a baixo:

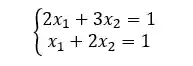
Podemos representa-lo através de matrizes, mas como?!

Na forma matricial, uma equação qualquer do sistema linear é representado assim:

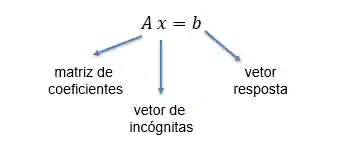
Se olharmos pro nosso sistema linear de exemplo podemos escrever o vetor de incógnitas:

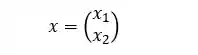
Seguindo a mesma lógica podemos escrever a matriz de coeficientes, , e o vetor de respostas :

Então finalmente, juntando tudo:

Viu! Tranquilinho 😉

Matriz Aumentada

Há uma outra matriz importante, que chamamos de matriz aumentada. Ela é quase igual à matriz de coeficientes, só que com uma coluna a mais. Nessa última coluna, à direita, colocamos o vetor .

Veja só a matriz aumentada do sistema que mostramos acima:

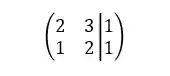
Maneira essa forma de representação matricial não é mesmo?

Agora vamos resolver o nosso exemplo!

Como resolver um sistema linear com matrizes?

Vamos pegar a nossa matriz aumentada, olhar para a primeira linha e escolher um pivô. Tudo que estiver abaixo desse pivô deverá ser zerado, para isso podemos usar operações básicas como soma e multiplicação!

O que vamos fazer aqui é escalonar a matriz!

Beleza, então vamos zerar aquele em baixo do . Para isso vamos multiplicar a segunda linha por :

Agora somamos a primeira linha com a segunda:

Prontinho, esta escalonada!

Se escrevermos em forma de sistema linear, ficamos com:

Já fica bem mais fácil resolver o sistema:

Podemos também encontrar :

Agora que você já sabe como representar um sistema linear pela forma matricial e resolver um sistema linear usando a forma matricial eu preciso te falar, esse foi só o começo!

Mas calma, o RespondeAí tem tudo que você precisa! Para isso preparamos um RAIO-X! ⚡

Nele você encontra todo esse conteúdo de matrizes e sistemas lineares, que você precisa para arrebentar na prova, separado em capítulos e tópicos e assim você tem um estudo bem organizadinho! 😍😍😍

Está esperando o que pra conferir o Raio-X aqui embaixo? 👇🏽