Derivadas

Fala aí, bem vindo ao RespondeAí! A plataforma criada pra te ajudar a mandar bem nas suas provas sem precisar arrancar os cabelos!

Então bora aprender sobre derivadas de uma forma tranquila e descontraída?

Para não complicarmos nossas vidas vamos primeiro entender o conceito de Derivada para depois aprender como podemos resolvê-las na prática!

O que são derivadas?

A derivada é a taxa de variação de uma função!

-Opa, mas como assim?

Pra facilitar vamos usar um exemplo de derivada, que é a velocidade instantânea.

A velocidade instantânea é nada mais nada menos que a taxa da variação da distância percorrida em determinado tempo. Graficamente temos:

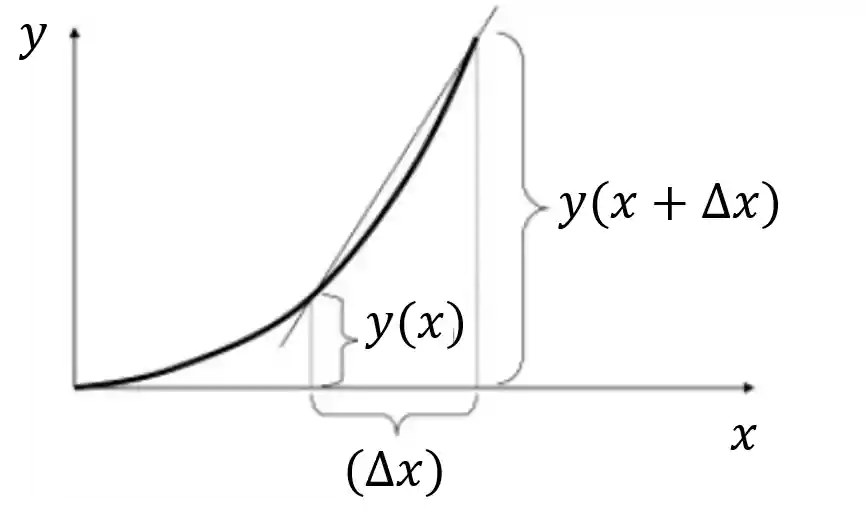
Se aproximarmos o de , ou seja pegamos um tempo beeeem pequenininho, próxima de zero e dividimos a distância percorrida por esse tempo, obtemos a taxa de variação da distância em função do tempo nesse ponto, ou seja, sua derivada que é a velocidade instantânea!

Então a velocidade média é a derivada da distância em relação ao tempo. Pegou o espirito da coisa?

Beleza, a gente já entendeu o que é a taxa de variação de uma função. Mas como calculamos a derivada de uma função?

A derivada por definição é dada pela seguinte expressão:

Lembra que falamos que , tem que ser bem pequenininho, próximo de ? Então matematicamente faz sentido termos o limite da expressão com tendendo a , certo?

Além disso, podemos observar que na nossa expressão temos a variação de divida pela variação de . Isso te lembra a alguma coisa?

Se você respondeu tangente ou coeficiente angular você acertou em cheio!

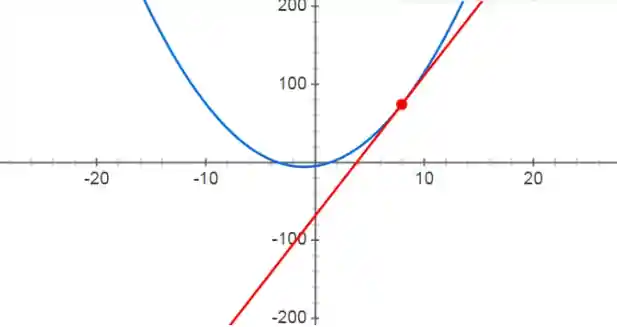
Na figura acima podemos ver a derivada da função em um ponto. E podemos perceber que a derivada determina a inclinação da reta desse ponto!

Agora que você começou a entender o que é uma derivada, você pode entender um pouco mais a fundo em definição de derivadas e verificar suas principais propriedades. Aqui no assunto de Derivadas também falamos sobre derivadas de diferentes funções, regras, métodos de derivação e mais!

Também temos a Calculadora de Derivadas pra ser sua companheira de guerra!

Aqui em baixo temos um Raio-X repleto de tópicos sobre Derivadas para facilitar ainda mais os seus estudos! Venha para o RespondeAí e tenha acesso a todo nosso conteúdo, com exercícios, listas resolvidas passo a passo, em vídeo, aulões, e mais!

Mande bem na sua prova de Cálculo, assine o RespondeAí!