Integral de Superfície

Olá universitário guerreiro haha. Nós somos o Responde Aí, a plataforma de exatas criada para levar até você um ensino didático e descontraído, e com a gente o seu semestre está salvo.

As integrais são um conteúdo muito importante no cálculo, tanto que elas se fazem presente desde o cálculo 1. Hoje nós estamos aqui para introduzir para você um tipo específico de integral, que chamamos de integral de superfície. Partiu?

Conhecimentos Prévios

Bom, os conhecimentos dentro do cálculo acabam sendo bem acumulativos, ou seja, uma coisa que você aprendeu antes vai ser usada no que você está aprendendo agora. Por isso, é importante que você tenha em mente que para iniciar o assunto de integral de superfície é bom você estar safo nesses assuntos anteriores:

☑️ Curvas e Superfícies

☑️ Integrais Duplas

Aconselho você a dá uma olhadinha nesses assuntos, para dá aquela refrescada na mente, combinado?

O que é Integral de Superfície?

Então vamos para o que interessa hahaha. Afinal, o que é uma integral de superfície?

Uma integral de superfície segue um princípio semelhante ao das integrais duplas. Nas integrais duplas nós pegamos uma função e integramos ela em um intervalo de e em um intervalo de . No caso das integrais de superfície nós vamos estar interessados em pegar uma função e integrar ela em uma superfície no plano e não mais em um intervalo, sacou?

No caso das integrais de superfície nós não teremos uma função de duas variáveis, teremos uma função , ou seja, uma função de variáveis.

Representamos uma integral de superfície do seguinte modo:

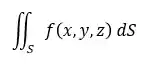
Onde é a superfície sobre a qual vamos integrar e é o elemento infinitesimal, assim como temos o na integral dupla.

A integral de superfície muitas vezes representa o cálculo da área da superfície. Imagina que temos um plano no .

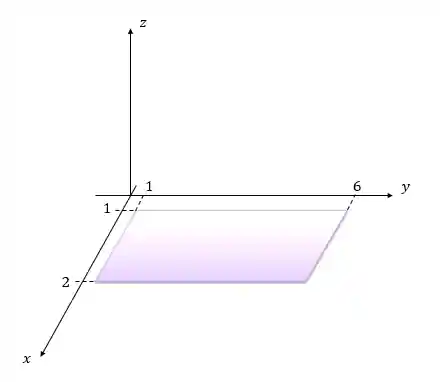
E queremos integrar uma função sobre esse plano.

Olhando a imagem, o nosso elemento infinitesimal pode ser escrito como , com o variando de a e o variando de a e, assim temos a seguinte expressão para o cálculo da integral de superfície:

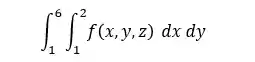
Beleza, mas o que acontece se a função for constante e igual a ?

Vamos calcular a integral de superfície para esse caso, e para isso basta resolvemos uma integral dupla:

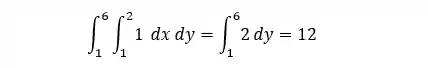
Note que esse valor que encontramos para a integral de superfície é exatamente o valor da área do plano .

Então, quando a função dentro da integral de superfície é igual a nós temos como resultado a área da superfície. Irado, não é?

Essa foi só uma introdução sobre integral de superfície pra você ter um gostinho do que vai aprender dentro desse assunto, mas tem muito mais coisas interessantes para saber, como por exemplo, como calcular uma integral de superfície quando tivermos uma função genérica.

Ficou curioso? Calma que nós pensamos em tudo. Nós preparamos o que chamamos de Raio-X, onde separamos todo o conteúdo que você precisa saber dentro do assunto de integral de superfície em capítulos e tópicos. Desse modo o seu estudo é direcionado, seguindo uma ordem lógica e claro que bem descontraído e didático porque você está no Responde Aí haha

Confere o nosso Raio-X aqui embaixo 👇🏽 e partiu ser aprovado com o Responde Aí 😉