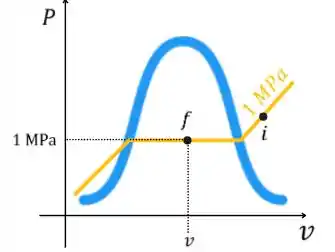
Um arranjo pistão-cilindro contém de vapor d’água a e . O vapor é resfriado a pressão constante até que metade da massa condense.
- Mostre o processo em um diagrama P-v.
- Encontre a temperatura final.
- Determine a variação de volume.
Passo 1
Primeiramente, precisamos analisar os dados. Temos vapor d’água a e que será condensada pela metade, logo a substância está resfriando. Logo temos inicialmente vapor superaquecido e no final temos vapor saturado.
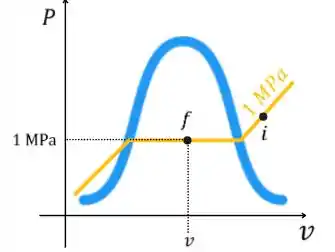
Passo 2
Segundo o enunciado, metade da massa irá se condensar. Dessa forma, teremos uma mistura de líquido e vapor, ou seja, vapor saturado. Como a pressão se mantém constante vamos utilizá-la para encontrar a temperatura de saturação do fluido.
Pela Tabela A-5 a , temos:
Passo 3
Para determinar a variação de volume precisamos encontrar o volume específico, tanto do estado inicial, quanto do final. Obteremos esses valores nas Tabelas A-6 e A-5, respectivamente.
Para o primeiro estado, que é vapor superaquecido, teremos:
Com os valores acima encontramos pela tabela:
Para o segundo estado, que é vapor saturado, teremos:
Logo, pela tabela teremos:
Podemos utilizar a fórmula de volume específico, expressa abaixo, para obter o , pois nesta fase a substância é composta por vapor e líquido. Assim, ela possui um valor de título que é de e pode ser calculada pela fórmula.