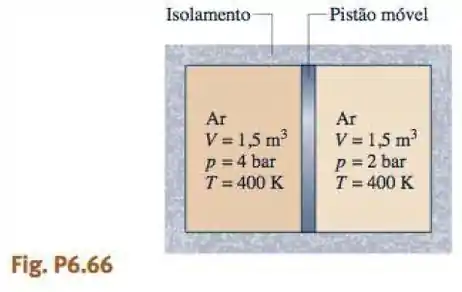
Conforme o ilustrado na Fig. , uma caixa isolada é inicialmente dividida em duas metades por um pistão condutor térmico e com atrito desprezível. Em um dos lados do pistão, há de ar a , . No outro lado, há de ar a , . O pistão é liberado e o equilíbrio é atingido, sem o pistão experimentar qualquer mudança de estado. Empregando o modelo de gás ideal para o ar, determine
(a) a temperatura final, em .
(b) a pressão final, em bar.
(c) a quantidade de entropia gerada, em .
Passo 1
E aí, tudo bem? Bora matar essa questão, mas para isso vamos pra nossas considerações!
O sistema engloba a quantidade total de Ar e o pistão
O sistema é isolado ou seja
O pistão se move livremente no cilindro e conduz termicamente
Passo 2
a)
Agora que temos nossas considerações, vamos fazer o balanço de energia lembrando que o sistema e fechado logo não tem troca de calor nem trabalho sendo realizado!
Da consideração temos:
Organizando temos:
Isolando :
Passo 3
b)
Agora usando a equação do gás ideal temos:
Onde:
Agora pra finalizar esse item temos:
Passo 4
c)
Pra matar de vez vamos fazer o balanço de entropia!
Como e :
Reorganizando temos:
Agora substituindo:
Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta
𝑎)
b)
c)