Resolva o problema 9.3 em uma base de ar-padrão frio com calores específicos avaliados a 300 K
Passo 1
Falaaa galerinha, beleza? Show, dentro do ciclo:
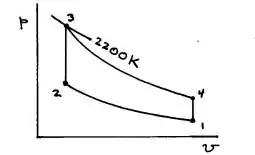
Vamos começar a calcular as propriedades em cada estado. Começando pelo 1, a questão já nos deu a pressão e a temperatura inicial.
No estado 2, para uma compressão isentrópica:
No estado 3, temos a temperatura máxima T3=2200K, dado pela questão.
E por fim, no estado 4 para uma compressão isentrópica:
Onde k é dado na tabela A-20 (k=1.4)
Passo 2
Belezura, bora começar a calcular o que a questão pede. No item a), para encontrarmos a adição de calor, temos:
Logo,
E essa é a adição de calor (do estado 2 para o estado de max temperatura (3)). No item b), o trabalho pode ser calculado como:
No item c) Para calcularmos a eficiência térmica, dividimos o trabalho do ciclo pera quantidade de calor na transformação do estado 2 para o 3, logo:
No item d), a pressão efetiva é calculada como:
Resposta
Resposta nos passos