Considera um sistema de partículas distinguíveis distribuídas em dois níveis não degenerados separados por uma energia e em equilíbrio com um reservatório a uma temperatura Calcule,
a) a função partição;
b) as frações de partículas em cada estado;
c) a energia interna do sistema;
d) a entropia do sistema;
e) o calor específico do sistema;
f) faça esboços de em função de
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears considere um sistema de partículas distinguíveis distribuídas em dois níveis não degenerados separados por uma energia e em equilíbrio com um reservatório a uma temperatura Calcule,
a) a função partição;
b) as frações de partículas em cada estado;
c) a energia interna do sistema;
d) a entropia do sistema;
e) o calor específico do sistema;
f) faça esboços de em função de

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha antes de determinar os abaixo, temos
Ficando na letra (a) para função partição,
Já na letra (b) para determinarmos as frações temos,
Ficando sua definição geral como,
Na letra para determinarmos a energia temos,
Que substituindo representa,
Ficando,
Passo 3
Já na letra (d) para a entropia do sistema,
Ficando,
Na letra (e) para determinarmos o calor específico de temos,
Ficando,
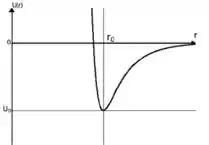
E por fim na letra (f) definindo o esboço de temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d)
e)
f) gráfico definido no passo anterior.
.