Considere um rio escoando em direção a um lago com uma velocidade média de a uma vazão de em um local acima da superfície do lago. Determine a energia mecânica total da água do rio por unidade de massa e o potencial para geração de potência do rio naquele local.
Passo 1
O problema envolve o escoamento de um rio, que produz energia elétrica a partir da energia mecânica da água. Temos então, uma velocidade, uma vazão e uma altitude, apresentados no enunciado. Devemos determinar a energia mecânica total da água do rio por unidade de massa e o potencial para geração de potência do rio naquele local. Tranquilo até aqui?

Na figura abaixo temos o esquema para o entendimento do exercício:
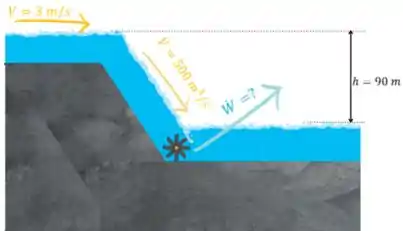
Temos como dados:
- , que é a velocidade de escoamento do rio;
- , que é a vazão volumétrica do rio, ou seja, o volume de água que passa a cada segundo;
- , é a potência que queremos determinar;
- , será a energia mecânica por unidade de massa que vamos determinar;
- , é a altura da queda d’água.
Entendido isso, podemos iniciar os cálculos.
Passo 2
Primeiramente, vamos calcular a energia mecânica por unidade de massa. Essa energia corresponde a energia total presente na água e pode ser escrita como:
A energia cinética é proveniente do movimento da água e a energia potencial é a parcela que depende da altura da queda d’água. Temos então:
Temos então:
Agora podemos substituir os valores:
Passo 3
Vamos calcular agora o potencial para geração de potência no rio. O potencial de geração é obtido pela seguinte multiplicação:
A água possui . Para obter a vazão mássica, temos:
Então:
Substituindo em , temos:
Convertendo para , temos:
Até a próxima, pessoal!
