Considere uma usina de potência a vapor operando entre os limites de pressão de e . Vapor d’água entra na bomba como líquido saturado e sai da turbina como vapor saturado. Determine a razão entre o trabalho produzido pela turbina e o trabalho consumido pela bomba. Assuma que todo ciclo seja reversível e que as perdas de calor da bomba e da turbina sejam desprezíveis.
Passo 1
E aí, galera! Vamos resolver essa questão?
Pela Tabela A-5, temos:
Temos que:
e
Então, temos na mesma tabela:
Para o terceiro estado temos:
Vamos interpolar na Tabela A-6:
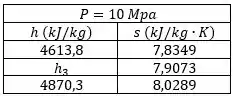
Para calcular o trabalho que sai, temos:
Substituindo valores:
A expressão para determinar o trabalho que entra é:
Como , pois não temos energia potencial e cinética a expressão torna-se:
Integrando, temos:
Substituindo valores:
Finalmente,
Entendido?
