Uma dada quantidade de monóxido de carbono é aquecida de a em um recipiente rígido a . Determine a pressão final do monóxido de carbono tratando-o como (a) um gás ideal e (b) um gás de Benedict-Webb-Rubin.
Passo 1
Okay galera, vamos lá! O monóxido de carbono é aquecido em um recipiente rígido. A pressão final do CO deve ser determinada usando a equação de idéia e a equação de estado de Benedict-Webb-Rubin. (a) Da equação do gás ideal,
Passo 2
(b) O volume molar específico do é

Usando os coeficientes da Tabela 3-4 para o e os dados fornecidos, a equação de estado de Benedict-Webb-Rubin para o estado 2 dá,
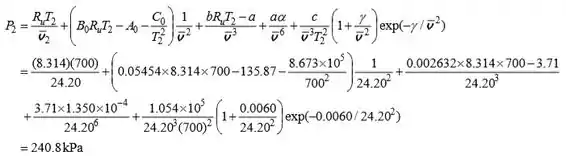
A pressão na unidade em inglês é
