A demanda total de vapor d'água de uma planta por um período de uma hora é de , porém a demanda instantânea flutua de a . Uma operação em regime estacionário da caldeira é aproximada pela inclusão de um acumulador, essencialmente um tanque contendo principalmente água líquida saturada que funciona como um "pulmão" entre a caldeira e a planta. A caldeira produz vapor saturado a 1.000.kPa e a planta opera com vapor a . Uma válvula de controle regula a pressã̉o do vapor na entrada do acumulador (saída da caldeira) e uma segunda válvula de controle regula a pressão na saida do acumulador (alimentação da planta). Quando a demanda de vapor é menor do que a quantidade produzida na caldeira, vapor entra no acumulador e é condensado pelo líquido existente no seu interior, causando um aumento da pressão para valores superiores aos . Quando a demanda de vapor é maior do que a quantidade produzida pela caldeira, água no acumulador vaporiza e vapor escoa para fora do acumulador, reduzindo a pressão para valores inferiores aos . Qual o volume necessário para o acumulador, de modo que esse serviço seja realizado com não mais de de seu volume ocupado por líquido?

Sob as condições estabelecidas, o pior ciclo possível de demanda pode ser representado da seguinte forma:

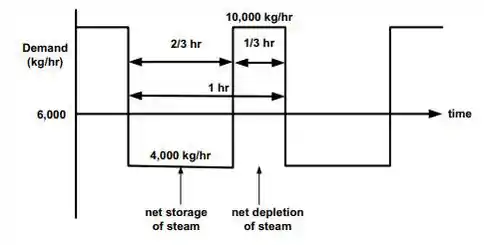
Essa situação pode ser representada como

onde θ = tempo de armazenamento de líquido

solução dá

O vapor armazenado durante esta perna é:

Consideramos esta perna de armazenamento e, para este processo de adição de vapor a um tanque, a equação desenvolvida no Problema 6-74 é aplicável:

Podemos substituir por , e rearranjar para

Contudo

Fazendo essa substituição e reorganizando, obtemos

Nesta equação, podemos determinar a partir das informações fornecidas tudo, exceto e Essas quantidades são expressas por

Portanto essa equação se torna (com )

Nesta equação, apenas x1 é desconhecido e podemos resolvê-lo da seguinte maneira. Primeiro, precisamos de V2

A partir das informações fornecidas, podemos escrever:

Portanto ou

Então (eqc)

Agora precisamos de valores de propriedade:

O estado inicial no acumulador é vapor úmido a 700kPa.

Encontramos nas mesas de vapor

O estado final no acumulador é vapor úmido a 1000kPa.

Das mesas de vapor

Resolva Eq(c) por

Resolva a próxima eq(b) para acho:

Dados

Então

Eq(A) dá e

Resolva para m1 e m2 usando um bloco de resolução Mathcad:

Acho:

Dados:

Finalmente, encontre o volume do tanque

Observe que apenas para armazenar 1.333,3 kg de vapor saturado a 1000kPa exigiria um volume de:

Pode-se resolver esse problema de maneira muito simples e quase correta, ignorando o vapor presente. Pela primeira equação do problema 3-15

Dados