Para o exemplo ilustrado na Figura 11.4, ache:
a) a probabilidade termodinâmica de cada macroestado,
b) o número total de microestados do conjunto ;
c) o número de ocupação médio de cada nível;
d) a soma dos números de ocupação médios.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears Para o exemplo ilustrado na Figura 11.4, ache:
a) a probabilidade termodinâmica de cada macroestado,
b) o número total de microestados do conjunto ;
c) o número de ocupação médio de cada nível;
d) a soma dos números de ocupação médios.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha primeiro vamos destacar a imagem abaixo por,
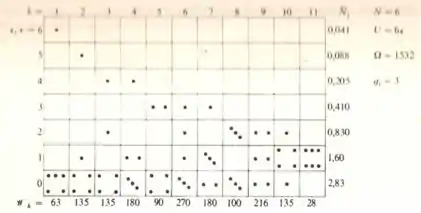
Com os macroestados possíveis de um conjunto de 6 partículas que obedece a estatística de Bose-Einstein, ficando na letra (a) para determinar a probabilidade termodinâmica de macroestado, temos
Ficando,
Chegando em,
Já na letra (b) para determinar o número de macroestado num conjunto
Sendo a soma do macroestado representado por,
Passo 3
Já na letra para se determinar o número de ocupação média de cada nível temos,
Com a entalpia igual e assim,
Podendo ser descrita como,
E por fim na letra (d) para determinar o número de ocupação média temos,
Sendo o sistema clássico obedecendo o termo,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d)
.