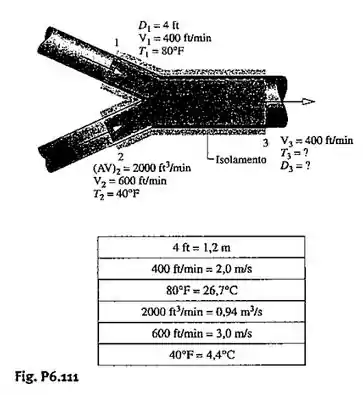
A Fig.P6.111 mostra uma parte dos dutos de um sistema de ventilação operando em regime permanente. Os dutos são bem isolados e a pressão é muito próxima a em todo o conjunto. Admitindo o modelo de gás ideal para o ar com e os efeitos das energias cinética e potencial, determine:
a) a temperatura do ar na saída, em .
b) o diâmetro na saída, em .
c) a taxa de geração de entropia no interior do duto, em .
Passo 1
Opa, tudo bem:
Vem comigo que vamos começar a resolver mais uma questão juntos!
Letra a)
Começamos o nosso problema aplicando um balanço de massa:
Aplicando um balando de taxa de energia:
Como e os efeitos da energia cinética e potencial sendo desprezados, temos:
Rearranjando:
Sendo as energias potencial e cinética desprezíveis:
Da equação dos gases ideais:
Pela equação de fluxo mássico:
Substituindo os dados:
Em 2:
Substituindo os valores na nossa equação de taxa de energia:
Passo 2
Letra b)
Calculando o diâmetro de saída:
Assim:
Substituindo os dados:
Passo 3
Letra c)
Aplicando a equação de taxa de geração de entropia:
Como e abrindo :
Abrindo:
Como a pressão é constante:
Substituindo os dados:
Te espero na próxima questão!