Equação de Soave/Redlich/Kwong :
Ω : = 0.08664
Ψ : = 0.42748
c : = b . 480 + 1.574 ) ⋅ ω - 0.176 ⋅ ω 2 ¯
α : = 1 + c ⋅ ( l - T r ) 0.5 2
β Ω = P r T r → Eq. 3.53
q : = Ψ α Ω ⋅ T r → E q 3.54
Achado:
z : = 1
Dados
z = 1 + β - q ⋅ β ⋅ z - β z ⋅ ( z + β )
Eq 3.52
Z ( β , q ) : = e n c o n t r e ( z )
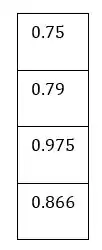
i : = 1 … 4
I i : = l n Z β i , q i + β i Z β i , q i )
Eq6.65b
H R i : = R ⋅ T 1 i Z β i , q i ) - 1 - c i ⋅ T r i α i 0.5 + 1 ⋅ q i ⋅ I i
Eq6.67
S R i : = R ⋅ l n z β i , q i ) - β i - c i ) ⋅ T r i α i 0.5 ⋅ q i ⋅ I i
A derivada nessas equações é igual a:
- c i ⋅ T r i α i 0.5
Agora iterate para T2
T2 : = 273 ) 300 232 384 K
Z β i , q i
)
H R = - 2.936 - 2.356 - 0.526 - 1.523 k J m o l
S R = - 6.126 - 4.769 - 1.789 - 2.679 J m o l ⋅ K
τ : = T 2 → T 1
Cp : = R ⋅ A + B 2 ⋅ T 1 ⋅ ( ) + 1 + C 3 ⋅ π 1 2 ⋅ ( ) 2 + τ + 1 + D τ ⋅ T 1 2
T 2 : = H R C p + T 1 →
T 2 = 272.757 ) 299.741 231.873 383.554 K
Δ S : = C p ⋅ l n T 2 T 1 - R ⋅ l n P 2 P 1 - S R ¯
Δ S = 31.565 30.028 32.128 22.18
J m o l ⋅ K