Um gás em condições a montante do estrangulamento iguais a é estrangulado para uma pressão a jusante de 1,2 bar. Use a equação de Redlich/Kwong para estimar a temperatura a jusante e o do gás para uma das seguintes opções:
(a) Dióxido de carbono, com e bar.(b) Etileno, e bar.(c) Nitrogênio, com bar.(d) Propano, com e bar.
Passo 1
Faala ae, tudo bem?? Bora resolver essa questão bem rápida!
K
Como no Exemplo 7.4, Eq. (6.93) é aplicado a este processo de entalpia constante. Se o estado final em 1,2 bar for considerado um gás ideal, então a Eq. (A) do Exemplo 7.4 (pág. 265) se aplica. Seu uso requer expressões para HR e Cp nas condições iniciais.
Passo 2
Equação de Redlich / Kwong:
Acho:
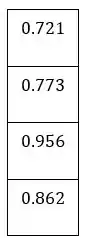
Dados
O procedimento mais simples aqui é iterar adivinhando T2 e, em seguida, calculando-o.
Achados K
)