a) mostre que a entropia de um conjunto de osciladores de Einstein é dada por
b) mostre que a entropia se aproxima de zero quanto se aproxima de zero;
c) que entropia se aproxima de quando é grande;
d) faça um gráfico de contra
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears ele vamos colocar o que ele pede sendo dividido pelas seguintes opções:
a) mostre que a entropia de um conjunto de osciladores de Einstein é dada por
b) mostre que a entropia se aproxima de zero quanto se aproxima de zero;
c) que entropia se aproxima de quando é grande;
d) faça um gráfico de contra

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera começando essa questão pela letra (a) que vem definindo a entropia de um conjunto de osciladores de Einstein que é representado por
Temos que a teoria de Einstein de inicio pode ser definida por,
Onde sua temperata é definida como:
Ficando sua definição representada por,
A partir daí tendo como o termo de subconjunto a equação:
Vamos ter o subconjunto representado por,
Passo 3
Já na letra (b) para mostrar que a entropia se aproxima de zero vamos ter,
Com , temos
Ficando,
E por fim na letra para se determinar a entropia que se aproxima de , temos
Que fica,
E por fim na letra (d) definindo o gráfico de contra , temos
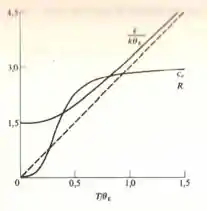
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d) gráfico destacado no passo anterior.
.