a) mostre que o número de moléculas com velocidades escalares menores que um valor arbitrário dado por
onde são definidos no problema anterior,
b) mostre que o número de moléculas com velocidades escalares maiores que um valor arbitrário é dado por,
Calcule a fração das moléculas com velocidades escalares entre,
c)
d)
e)
f) ilustre sua resposta graficamente em termos da função distribuição de velocidades escalares.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears ele deseja determinar:
a) mostre que o número de moléculas com velocidades escalares menores que um valor arbitrário dado por
onde são definidos no problema anterior,
b) mostre que o número de moléculas com velocidades escalares maiores que um valor arbitrário é dado por,
Calcule a fração das moléculas com velocidades escalares entre,
c)
d)
e)
f) ilustre sua resposta graficamente em termos da função distribuição de velocidades escalares.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera para mostrarmos que o número de moléculas com velocidades escales são menores que um valor arbitrário temos,
Assim,
Já na para a letra (b) em que ele pede para mostrar o número de moléculas com velocidades escalares temos
Ficando,
Passo 3
Já para a letra para determinarmos a velocidade escalar entre
Na letra (d) a velocidade escalar entre vai ser,
Na letra (e) para a velocidade escalar entre temos,
E por fim na letra (f) a sua ilustração gráfica pode ser definida por,
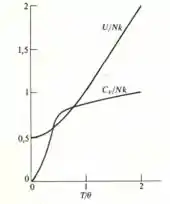
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d)
e)
f) gráfico ilustrado no passo anterior
.