Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 169
As necessidades de ar comprimido de uma fábrica ao nível do mar são atendidas por um compressor de que recebe o ar a uma pressão atmosférica de e a uma temperatura média de , comprimindo-o ate . Uma análise do sistema de ar comprimido e do equipamento que o utiliza revela que a compressão do ar até e suficiente para essa fábrica. O compressor opera a da carga nominal e e acionado por um motor elétrico com de eficiencia. Considerando que o preço da eletricidade e de , determine a quantidade de energia e o dinheiro que se economizara como resultado da redução da pressão do ar comprimido.
Passo 1
Vamos lá! A questão nos afirma que as necessidades de ar comprimido de uma planta estão sendo atendidas por um compressor de que comprime ar de a . A quantidade de energia e dinheiro economizados pela redução da pressão do ar comprimido para deve ser determinada.
Podemos representar como,
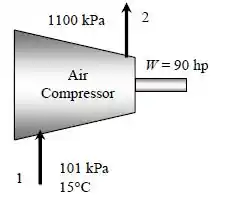
Assumindo que:
- O ar é um gás ideal com aquecimento específico constante.
- As mudanças cinéticas e potenciais de energia são insignificantes.
- Fator de carga do compressor é dado para ser .
- As pressões indicadas são de pressão absoluta e não de pressão de gaje.
A razão de calor específica do ar é (Tabela A-2).
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que a energia elétrica consumida por este compressor por ano é
Passo 3
A fração de energia economizada como resultado da redução do ajuste da pressão do compressor é
Ou seja, a redução da pressão de ajuste resultará em cerca de de economia da energia consumida pelo compressor e do custo associado. Portanto, a economia de energia e custo, neste caso, torna-se
Portanto, a redução da pressão ajustada em resultará em uma economia anual de que, neste caso, vale .
Note que, algumas aplicações requerem ar comprimido a muito baixa pressão. Nesses casos, a necessidade pode ser atendida por um soprador em vez de um compressor. Desta forma, pode-se economizar energia considerável, já que um soprador requer uma pequena fração da energia necessária por um compressor para uma determinada vazão de massa.