Uma parede plana composta consiste em uma camada de isolante de 75 mm de espessura ( 0,05 W/m.K) e uma camada de tijolos de 25 mm de espessura ( 0,10 W/m.K). A temperatura interna relativa ao isolante é 20 °C. A temperatura externa dos tijolos é -13 °C. Determine, em regime permanente, (a) a temperatura na interface entre as duas camadas, em °C, e (b) a taxa de transferência de calor através da parede, em W por m² de área de superfície.
Passo 1
Primeiro vamos considerar algumas hipóteses importantes:
1 – O processo na parede ocorre em regime permanente.
2 – A temperatura varia linearmente através da parede.
3 – As duas paredes estão em contato térmico perfeito, sem perdas.
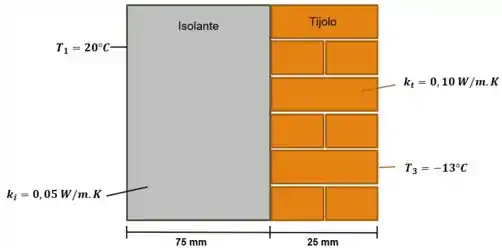
Arrumando um pouco os dados, temos:
Passo 2
Pela hipótese 3, toda transferência de calor que ocorre por condução dentro da parede de gesso passa também por condução para a parede de concreto. Então vamos ter:
Pela hipótese 1 e 2, temos:
Vamos chamar a temperatura intermediária entre as duas paredes de .
Para o isolante:
Para a parede de tijolo:
Igualando ambas as equações:
Vamos isolar para poder achar seu valor:
Substituindo as variáveis pelos dados:
Passo 3
Pronto! Nós temos a equação:
E na letra (b) é pedido !
Então só substituir os dados e achar a relação: